Как использовать золотое сечение в жизни. Золотое сечение: как это работает.

Как использовать золотое сечение в жизни. Золотое сечение: как это работает.

Золотое сечение это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве - во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Золотое сечение это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве - во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Определение.
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина - 1, 6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение в формах пространства и времени действует.

Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как "Ассиметричную Симметрию", называя его в широком смысле универсальным правилом отражающим структуру и порядок нашего мироустройства.

История.
Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах лука пачоли в книге "Божественная Пропорция" (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял сына, большой - отца, а целое - святой дух.

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 0, 1, 1, 2, 3. и т. д. на отношение этой последовательности к золотой пропорции обратил внимание Кеплер: "Устроена она так, что два Младших Члена Этой Нескончаемой Пропорции в Сумме Дают Третий Член, а Любые два Последних Члена, Если их Сложить, Дают Следующий Член, Причем та же Пропорция Сохраняется до Бесконечности". Сейчас ряд Фибоначчи это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его "Математическое Эстетство" вызывало много критики.

Природа.
Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

Белорусский ученый Эдуард сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль "Кривой Жизни". Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение днк и даже структура галактик заключают в себе ряд Фибоначчи.

Человек.
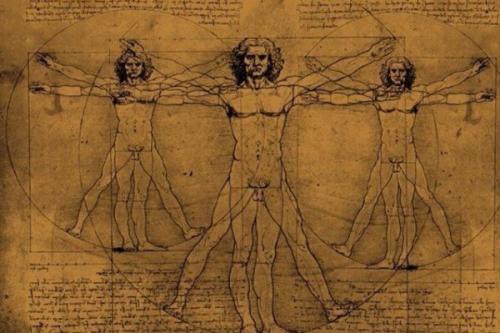
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек - это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.

В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле корбюзье, используя "Витрувианского Человека" Леонардо, создал собственную шкалу "гармонических пропорций", повлиявшую на эстетику архитектуры XX века.

Адольф цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.
В результате измерений исследователь установил, что пропорции мужского тела 13: 8 ближе к золотому сечению, чем пропорции женского тела - 8: 5.

Искусство пространственных форм.
Художник Василий суриков говорил, "что в Композиции Есть Непреложный Закон, Когда в Картине Нельзя Ничего ни Убрать, ни Добавить, Даже Лишнюю Точку Поставить Нельзя, это Настоящая Математика". Долгое время художники следователи этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.

Искусствовед Ф. в. Ковалев, подробно исследовав картину Николая Ге "Александр Сергеевич Пушкин в Селе Михайловском", отмечает, что каждая деталь полотна будь - то камин, этажерка, кресло или сам поэт строго вписаны в золотые пропорции.

Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке великие пирамиды гизы, собор парижской богоматери, храм Василия блаженного, Парфенон.
И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

Слово, звук и кинолента.
Формы временно? Го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи - 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом "Пиковой Дамы" является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853: 535=1, 6) - это и есть точка золотого сечения.

Советский музыковед э. к. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.
Кинорежиссер Сергей эйзенштейн сценарий своего фильма "Броненосец Потёмкин" сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух - в Одессе. Переход на сцены в городе и есть золотая середина фильма.

Золотое сечение в искусстве доклад. Что такое золотое сечение в искусстве?

Золотое сечение представляет собой деление отрезка на две неравные части. Оно производится таким образом, что меньшая из этих частей относится к большей так же, как большая к длине всего отрезка. Для рисунка 1 пропорция может быть записана следующей формулой: a:b=b:c.

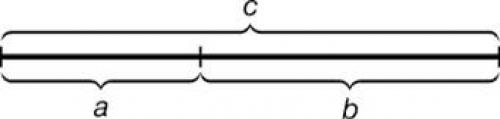Рисунок 1. Золотое сечение на примере отрезка.

Само понятие определяется при помощи терминов математики, однако на протяжении истории человечества это соотношение использовалось в науке и архитектуре. А золотое сечение в искусстве служит основой композиции в работах величайших мастеров прошлого. И сейчас оно остается одним из приемов, широко применяемых художниками, дизайнерами, фотографами и другими профессионалами творческой среды.

Простейшие пропорции в искусстве - примерное деление пространства на 3 части по вертикали и горизонтали, как показано на рисунке 2 . В случае с картинами или фотографиями на линиях и особенно в точках их пересечений располагаются композиционно значимые элементы.

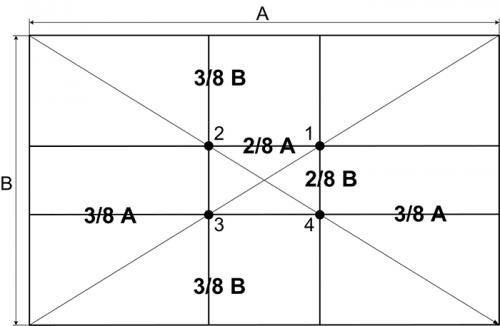Рисунок 2. Золотое сечение и гармония в искусстве.

Использование золотой пропорции как одного из ключевых средств композиции этим не ограничивается. Для создания гармоничных произведений представители творческих профессий применяют также геометрические фигуры, построенные на основе этого принципа. Это треугольники, прямоугольники, звезды, спирали и т.д.

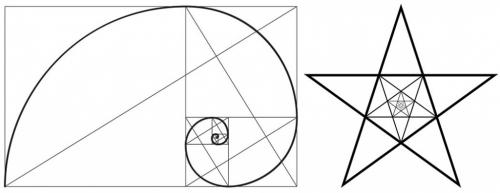Рисунок 3. Золотое сечение в спирали Архимеда и в последовательно вписанных пятиугольниках.

Но почему же именно такое соотношение выглядит лучше всего? Объект, в основе пропорций которого лежит принцип золотого сечения, визуально воспринимается как совершенный. Соотношение было подсмотрено у самой природы: оно присутствует в формах растений, животных и даже человеческого тела. Именно поэтому существует еще одно более поэтичное название «Божественная пропорция» . Но давайте посмотрим на конкретных примерах, как она вдохновляет художников на создание произведений искусства.

Польза. Значение слова «польза»

ПО́ЛЬЗА , -ы, ж.

1. Хороший результат, благоприятные последствия для кого-, чего-л. С пользой для дела. □ Университетская жизнь принесла ему мало пользы. Пушкин, Александр Радищев. Библиотекой, кроме Прозорова, никто не пользовался, и все эти дорогие издания в роскошных переплетах стояли в шкафах без всякой пользы. Мамин-Сибиряк, Горное гнездо.

2. Разг. устар. Нажива, барыш. — Изрядно торгуете, Татьяна Емельяновна? — Как сказать, батюшка. --- Оборот хотя и велик, но мы пользу берем небольшую, сами знаете. Эртель, Гарденины. Иногда дед мечтал: — Помог бы господь продать домишко этот, хоть с пятьюстами пользы, — отслужил бы я молебен Николе Угоднику. М. Горький, Детство.

◊

В пользу чью — 1) ради блага, выгоды кого-, чего-л. решил пожертвовать в пользу голодающих пять тысяч рублей серебром. Чехов, Жена. На следующий день --- был арестован и молодой Корыбко, поручик разведки Пилсудского, шпионивший также в пользу англичан. В. Беляев, Старая крепость; 2) с положительным результатом для кого-л. Николай, оглянувшись, заметил стоявшую у окна Нелидову --- и в ее пользу решил сравнение с вчерашней девицей. Л. Толстой, Хаджи-Мурат.
Говорить ( или свидетельствовать и т. п. ) в пользу кого-чего — 1) признавать, доказывать положительные качества, правоту кого-, чего-л. Пусть кто-нибудь осмелился б при мне Жену чужую соблазнить! Пусть слово Не в пользу б инквизиции сказал! А. К. Толстой, Дон Жуан; 2) перен. служить доказательством положительных качеств, правоты и т. п. кого-, чего-л. Беспокойная ласковость взгляда И поддельная краска ланит, И убогая роскошь наряда — Все не в пользу ее говорит. Н. Некрасов, Убогая и нарядная.
Идти на пользу — оказывать положительное действие, давать хорошие результаты.

Золотое сечение в технике. Введение

Высказывание известного авиаконструктора А.Н. Туполева стало «точкой отсчета» в моей работе. Действительно, человек всегда стремился к красоте и гармонии. Об этом много написано и сказано. Человек всегда стремился окружить себя красивыми вещами. А когда люди стали создавать сложные технические устройства, то понятие красоты в технике приобрело особое значение. Появляется специальная наука – эргономика, без основ которой сегодня невозможно создавать безопасные и эффективные системы, управляемые человеком. А самолет – это сложная техническая система.

В Internet-форумах (Опровергнем Туполева?, Авиационный форум AVIAFORUM.RU, Красиво? Значит, полетит" http://community.livejournal.com/ru_aviation/) идет оживленное обсуждение вопроса о том, какие самолеты можно считать красивыми, а какие нет. По каким критериям их классифицировать? Оказывается, довольно значительное количество людей интересуются этой проблемой. И вот, что я понял. Можно долго и многословно рассуждать о красоте и гармонии в искусстве, литературе, музыке и т.д. Если же рассуждения касаются инженерных и технических основ, то здесь становится ясно, что понятие красоты приобретет вполне определенный смысл. Мистика "золотого сечения" хороша для романов, но не для науки, заметил в своей статье В.С.Ярош. Эту же точку зрения высказывает в своей статье «Блеск «золотого» сечения» Игорь Ефремов: «В прикладных науках все подчинено главным образом целесообразности. Там роль «золотого» сечения, а также других мировых констант, неоспорима… для искусства «золотое» сечение может быть лишь начальным ориентиром… Задача учёного и инженера — строго соблюдать законы природы. Наука, оставаясь в рамках законов, говорит нам о том, что может быть. Искусство же больше связано с душой творца, чем с реальностью… Отступления от законов природы в технике просто вредны — устройство, построенное с отклонениями от законов естественных наук, и работать будет хуже (а, может, и вообще не будет), и эффективность его будет не велика. В искусстве же человеку дается шанс поупражняться в том, чего нет и быть не может». В одной из своих статей известный современный исследователь и поклонник теории «золотого» сечения, основатель «Академии Тринитаризма – Института Золотого Сечения – Математики Гармонии» Алексей Петрович Стахов высказал предположение, что Золотое Сечение является некоторым «метафизическим» знанием, «проточислом», «универсальным кодом Природы», который может стать основой для дальнейшего развития науки, в частности, математики, теоретической физики, генетики, компьютерной науки.

Золотое сечение, как построить. Просто о сложном: что это такое – правило золотого сечения

Золотое сечение –это правило общей пропорции, которая создает универсальную композицию. Математики называют её формулой божественной гармонии или асимметричной симметрией.

Это интересно!  Общее определение правила ЗС –меньшая величина относится к большей, как большая к целому. Было рассчитано приблизительное число, равное 1,6180339887, это и есть коэффициент золотого сечения. Если смотреть в процентном соотношении, то в одном целом меньшая величина занимает 38%, большая – 62%.

Признано считать, что ЗС пришло к нам еще с древней Греции, но есть и такое мнение, что его греки подсмотрели у египтян. Если проанализировать архитектуру Египта того времени, можно чётко проследить соблюдение математической гармонии. Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:

• практически все живые организмы можно привести к принципу числовой зависимости. Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
• данная зависимость чисел характерна только для биологических существ и кристаллов, все остальные неживые объекты природы крайне редко обладают золотой пропорцией;
• именно математическая пропорция в строении биологических объектов оказалась оптимальной для выживания.

Золотое сечение Леонардо да Винчи: что кроется в шифре?

В изображении "витрувианского человека" принято усматривать два тела - две фигуры, одна из которых вписывается в круг, а другая - в квадрат. Толкование такой композиции имеет следующее значение.

Квадрат - символ земного, таким образом автор отображает привязанность человека к земному, материальному. Центр квадрата находится в паховой области.

Круг - символ божественного, в том числе и божественного происхождения человека. Фигура, находящаяся в круге, не содержит черточек, то есть не измеряется. Поскольку как явление божественное, эта фигура и не может быть измерена. Центр окружности - пупок человека.

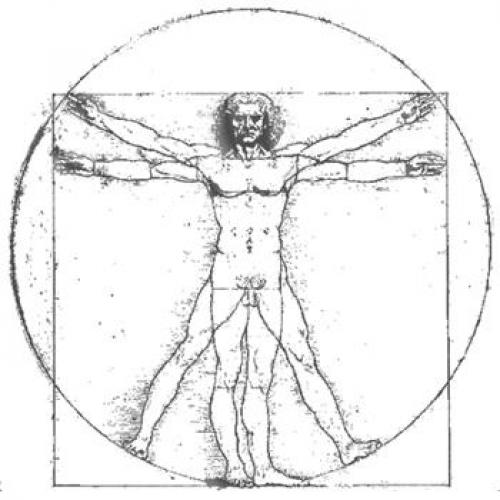
По современным представлениям, видеть только две фигуры в "витрувианском человеке" - слишком плоско. На самом деле в изображении можно рассмотреть гораздо больше. И это еще не все тайны, разгадываемые в этой загадке.

Внимание также обращается к ногам фигуры, стоящей в круге (божественное начало). Они стоят на плоскости, выходят за рамки окружности. В этом видится символ того, что человек тяготеет к земному, несмотря на божественную свою составляющую.

По материалам, оставленным Леонардо да Винчи, золотое сечение, кратко говоря, усматривается в человеческом теле. И опять-таки в изображении "витрувианского человека" заключено устремление людей того времени к возвышению. Великий гений узрел и попытался передать другим поколениям глубокий смысл, увиденный им в нашей природе.

Еще одно знаменитое творение, в котором отобразил Леонардо да Винчи золотое сечение, - "Мона Лиза". Ее загадочная улыбка невероятным образом очаровывает миллионы созерцателей.

Золотое сечение для детей. Золотое сечение в математике

Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.

В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:

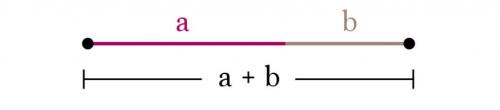
Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:

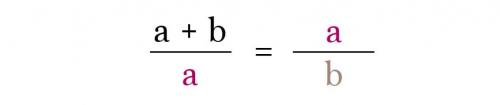
Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.

Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:

Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.

Видео ЗОЛОТОЕ СЕЧЕНИЕ