Парадокс монти холла.

Одна из ключевых сфер, в которых наш разум систематически ошибается - это вероятности, их вычисление и сравнение. Наш разум, действительно, имеет свойство давать неверные ответы на целый ряд вопросов о вероятностях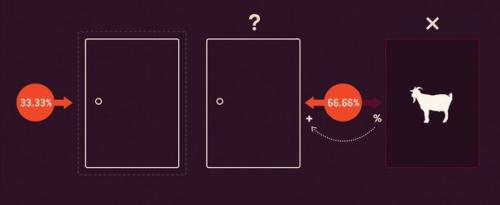
. А целый ряд эвристик (например, эвристика репрезентативности) и когнитивных искажений (например, кластерная иллюзия, игнорирование априорной вероятности, ошибка конъюнкции) являются, по сути, именно формой некомпетентности человеческого разума в оценке вероятностей и при осуществлении статистического вывода.

Причем ошибаются в сфере вероятностей не только обыватели, но даже специалисты, знакомые с теорией вероятности и математической статистики.

И, пожалуй, лучшей иллюстрацией тут может служить так называемый "Парадокс Монти Холла".

Что это за парадокс?

Давайте разберемся.

В популярном американском журнале "Парад" была авторская колонка под названием "спросите Мэрилин" (такого рода авторские колонки достаточно обычны для США. Вела колонку, конечно, не Мэрилин Монро, а Мэрилин вос савант. Почему именно она? Потому что она занесена в "Книгу Рекордов Гиннеса", как обладательница самого высокого в мире коэффициентом интеллекта (IQ) - целых 228! Эта колонка работала просто: люди присылали Мэрилин вос савант вопросы, а она отвечала.

И вот однажды (это был сентябрь 1990 года) ей прислали вопрос, по-видимому, навеянный телевикториной "На что Спорим", которую вел монти холл. Это телеведущий позже и "Подарил" свое имя рассматриваемому парадоксу.

Вопрос, присланный Мэрилин, был примерно таков:

"Дорогая Мэрилин, вот вам задача, соответствующая вашему феноменальному интеллекту.

Вы в телевикторине участвуете. Перед вами три двери, и вам надо выбрать одну из них. За одной дверью находится новенькая красная "Феррари", а за двумя другими дверями стоят живые козлы (вы не слышите, как они блеют или стучат копытами.

Вы одну из дверей выбрали.

И тут ведущий делает неожиданное - он открывает одну из дверей, которую вы не выбрали. За ней оказывается козел.

И затем хитрый шоумен говорит вам:

"Мэрилин! Это ваш шанс! Вы можете поменять свое решение и выбрать другую дверь. Сейчас или никогда! Так вот, стоит ли вам поддаться ведущему и поменять свой первоначальный выбор или нет?

С наилучшими пожеланиями, искренне ваш, аноним".

Я думаю, будет полезно, если вы, уважаемый читатель, тоже ответите на этот вопрос.

В том случае, если вы не знаете, что такое парадокс монти холла, не разбираетесь в теории вероятностей, то вы, скорее всего, ответите, что менять свой первоначальный выбор и выбирать другую дверь не стоит, так как это не меняет ваших шансов на выигрыш. Кроме того, скорее всего, вам будет неприятна сама идея о том, чтобы изменить ваше первоначальное решениепод влиянием, например, иллюзии контроля.

Но факт (и этот факт парадоксален) состоит в том, что если вы выберите другую дверь, то ваши шансы возрастут. Поэтому лучше свой первоначальный выбор изменить.

Таким образом, если вы ответили неправильно - не расстраивайтесь. Когда Мэрилин вос савант ответила правильно (стоит выбрать другую дверь), ее буквально завалили письмами, в которых упрекали ее в некомпетентности, глупости, незнании теории вероятностей. Причем, обратите внимание, критические письма ей писали даже специалисты - математики!

Да, не зря задачу с тремя дверьми называют парадоксом: действительно, трудно поверить, что надо поменять свое первоначальное решение и выбрать другую дверь.

Но с точки зрения теории вероятности тут все довольно просто. Давайте порассуждаем.

Какова вероятность того, что вы с первого раза выбрали дверь, за которой стоит новенькая красная "Феррари"?

Машина за одной из трех дверей находится. Следовательно, вероятность того, что вы угадали, за какой именно дверью находится машина, составляет 1/3 - один шанс из трех. Другими словами, если вы сыграете в эту игру много раз, то машина за выбранной вами дверью окажется в одном случае из трех. Обратите внимание! Вы угадаете не каждый третий раз, а в одном случае из трех. Т. е. из ста попыток вы угадаете в примерно тридцати трех случаях. Причем мы не знаем, как будут распределены эти случаи: возможно, угадывания и промахи будут чередоваться равномерно, или же вы сначала будете угадывать, а потом начнется полоса неудач, или же, наоборот, полоса неудач сменится чередой угадываний.

Итак, вероятность того, что вы угадали, составляет 1/3.

Но вероятность того, что вы не угадали, составляет 2/3. Вероятность того, что вы не угадали, выше, не правда ли?

Но это означает, что выше и вероятность того, что машина находится за другой дверью, за дверью, которую вы не выбрали.

Далее. В том случае, если бы ведущий не выводил из игры заведомо невыигрышную дверь, ваши шансы при смене решения так и остались бы на уровне "Один из Трех". Но ведущий открывает дверь с козлом, он исключает ее из ваших дальнейших попыток.

Соответственно, есть один шанс из трех, что выбранная вами дверь выигрышная и два шанса из трех, что машина стоит за другой дверью. Поэтому вам выгоднее поменять свое.