Меняются ли экваториальные координаты звезды в течение суток. Определение географических координат по звездам.

Меняются ли экваториальные координаты звезды в течение суток. Определение географических координат по звездам.

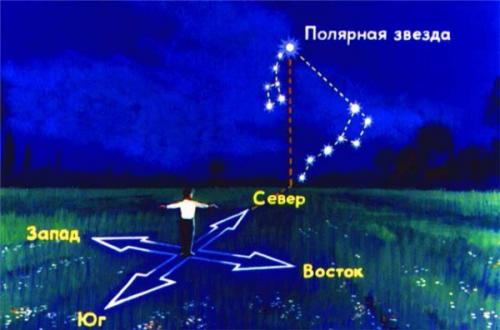
Я полагаю, вы знаете, что такое географические координаты и что высота полярной звезды над горизонтом приблизительно равна широте места наблюдения. Точнее - высота полюса мира, так как полярная находится не точно в точке полюса, а отстоит от него почти на градус. Значит, для измерения широты достаточно измерить высоту полюса мира. Давайте опять прочитаем отрывок из все того же "Таинственного Острова".

Сайрес смит возвратился в Трубы. При свете очага он обстругал две маленькие гладкие дощечки и соединил их концами, так что получилось нечто вроде циркуля с раздвижными ножками. Для скрепления послужил толстый шип акации, найденный среди хвороста.

На юге линия горизонта, освещенная снизу первыми лучами луны, резко выделялась на небе и могла быть определена с достаточной точностью. В эту минуту созвездие южного креста казалось наблюдателю опрокинутым, а альфа находилась в основании созвездия, более приближенном к южному полюсу.

Это созвездие расположено не так близко к антарктическому полюсу, как полярная звезда к полюсу арктическому. Звезда альфа от него примерно на двадцать семь градусов отстоит. Сайресу Смиту это было известно, и он должен был учитывать данное расстояние при своих вычислениях к тому же инженер наблюдал эту звезду в момент ее прохождения через нижний меридиан это значительно облегчало вычисления.

Сайрес Смит направил одну ножку своего циркуля на морской горизонт, другую - на звезду альфа и по расстоянию между ними определил угловое расстояние альфы от горизонта. Чтобы твердо зафиксировать полученный угол, он приколол шипами акации обе ножки прибора к третьей поперечной дощечке, так что расстояние между ними было твердо закреплено.

После сделанного оставалось лишь вычислить этот угол, с поправкой на высоту над уровнем моря и учитывая понижение горизонта. Для этого надо было определить высоту плато. Величина угла даст высоту звезды альфа, а следовательно, и полюса над горизонтом - то есть широту острова, ибо широта какой-либо точки на земном шаре всегда равна высоте полюса над горизонтом в этой точке.

Здесь тоже автор допустил ошибку - в это время года (описанные события происходят в апреле) южный крест около полуночи находится в верхней кульминации, а не в нижней, т. е. пересекает меридиан не ниже, а выше полюса и высота альфы превышает 60°. Но дело даже не в этом - чтобы пользоваться таким "Угломерным Инструментом" нужно быть, наверное, хамелеоном - во всяком случае, такой большой угол визировать с рук точно не получится. Прибор придется, как минимум, установить на какое-то подобие штатива. Кстати, намного проще и точнее было бы измерять не высоту звезды над горизонтом, а её зенитное расстояние (направление вертикали не нужно визировать - его легко получить с помощью отвеса).

К тому же я, житель северного полушария (как и герои Жюля верна), ни за что бы не вспомнил склонение альфы южного креста. А вы? Пожалуй, стоит подумать над другим способом - и этот способ известен еще с древних времен. Это определение широты по солнцу с помощью гномона.

Как и в предыдущей работе, определим высоту солнца - только на этот раз в момент полдня, когда тень гномона совпадает с полуденной линией (кстати, отметьте и точное время полдня - нам оно пригодится в дальнейшем.

Теперь главная проблема в определении широты - нахождение склонения солнца на момент наблюдений, причем желательно без компьютера (ведь мы на необитаемом острове. Думаю, даже феноменальная память сайреса Смита тут не поможет, значение этой величины придется посчитать, но - без расчетов!

Слонение солнца.

Мы знаем, что склонение солнца изменяется от - 23, 5° до 23, 5° (это наклон земной оси к эклиптике и широты линий тропиков, я надеюсь, что уж эти значения мы вспомним даже на необитаемом острове. Нам придется несколько упростить задачу и считать, что солнце движется по эклиптике равномерно. В этом случае склонение солнца приблизительно можно определить по формуле.

О = 23, 5°sin (D*360/365), где.

D - количество дней, прошедших после весеннего равноденствия.

Графически это можно сделать так:

Построим окружность радиусом 23, 5 единицы (что именно будет этой единицей измерения нам не важно - спичка, например, если придется рисовать на песке), разделим ее на 12 частей, как в предыдущей работе, только на этот раз деления будут изображать месяцы, точнее, интервалы в 30, 5 суток. Теперь нужно лишь отложить на окружности дату наших наблюдений, считая горизонтальную ось - линией равноденствий (21 марта и 22 сентября), а вертикальную - солнцестояний (22 июня и 22 декабря. Дату лучше откладывать от ближайшей из этих точек для уменьшения ошибок. Проекция найденной точки на вертикальную ось и даст значение склонения солнца? О - осталось только точно измерить его нашим "Эталоном Длины" - спичкой. Такое простое построение гарантирует определение склонения с точностью не хуже 1/2 градуса.

Определение широты по солнцу.

Теперь можно найти широту точки наблюдения - из рисунка видно, что.

=90°-h? О, где.

О - склонение солнца, h - высота солнца над горизонтом.

Теперь займемся долготой. Здесь без знания времени не обойтись, но, в отличие от жюльверновского XIX века, теперь точные часы не редкость, так что будем полагать, что нам известно время с ошибкой не более полминуты. На этот раз наша задача, кажется, очень проста - ведь долгота (в часовой мере) есть разность между местным и гринвичским временем. Осталось только определить гринвичское время. Но так как мы определяем момент полдня по солнцу, (т. е. по истинному солнечному времени) то и гринвичское время нам нужно тоже истинное солнечное. Наши же часы среднее поясное время показывают. Дело в том, что солнце движется по эклиптике неравномерно и продолжительность суток немного меняется на протяжении года, что, конечно, очень неудобно для счета времени. Поэтому и было принято "Равномерное" среднее солнечное время, которое определяется по воображаемой точке, совершенно равномерно движущейся по небесному экватору. Разница между средним и истинным солнечным временем может достигать 16 минут и называется уравнением времени. О нем мы поговорим в следующей главе, пока же будем считать, что эта поправка нам известна или мы наблюдаем в один из дней, когда среднее солнечное время совпадает с истинным - это происходит 4 раза в году - 16 апреля, 14 июня, 1 сентября и 25 декабря.

= tm -tгр = tm - (Tn - n ), где.

- Географическая долгота.

tгр - Истинное гринвичское солнечное время.

tm - истинное местное время.

Tn - среднее поясное время n - го часового пояса.

- Уравнение времени.

А в момент местного полдня.

= 12 ч -tгр = 12 ч - Tn n -?

(Долгота считается положительной к Востоку от Гринвича).

Номер часового пояса в этой формуле - целое число, показывающее, на сколько часов поясное время отличается от гринвичского. Так, Москва находится во втором часовом поясе, но в 30-е годы XX века было введено "Декретное" время, на час опережающее поясное, кроме того, летом стрелки часов переводятся еще на час вперед, следовательно, разница между московским и гринвичским временем составляет 3 часа зимой и 4 - летом.

Теперь мы можем определить гринвичское истинное солнечное время, а, следовательно, и географическую долготу места наблюдения.

А теперь снова посмотрим, как действовали герои Жюля верна:

- Сегодня пятнадцатое апреля, не правда ли?

- Да, мистер сайрес, - ответил юноша.

- В таком случае, завтра, если не ошибаюсь, наступит один из четырех дней в году, когда истинное время совпадает со средним. Иначе говоря, дитя мое, завтра солнце пересечет меридиан за несколько секунд до полудня. В случае если будет хорошая погода, мне, вероятно, удастся определить долготу нашего острова с приближением до нескольких градусов.

Сайрес Смит отыскал на берегу совершенно чистое место, хорошо выровненное отливом. Тонкий слой песка был гладок, как зеркало, песчинки лежали одна к одной, словно на подбор. Впрочем, этот слой мог быть не вполне горизонтальным, а воткнутая в него шестифутовая жердочка могла стоять и не совсем отвесно. Наоборот, инженер даже наклонил ее слегка к югу, то есть в противоположную от солнца сторону, ибо не следует забывать, что обитатели острова линкольна находились в южном полушарии и потому видели дневное светило не над южным, а над северным горизонтом.

Тут харберт понял, каким образом инженер собирается установить момент кульминации солнца или его прохождения через меридиан, то есть, другими словами, время полудня для данной местности. Этому должна была служить тень палочки на песке. Таким способом сайрес Смит без всяких инструментов мог получить достаточно точные результаты.

Действительно, в ту минуту, когда тень станет короче всего, будет ровно двенадцать часов дня. Наблюдателю оставалось только следить за концом тени, чтобы заметить, когда она снова начнет удлиняться. Наклонив жердь к югу, Смит увеличил размеры тени, чтобы легче было наблюдать за ее изменениями. Ведь чем крупнее стрелка часов, тем заметнее ее движение. А тень жердочки на песке была, в сущности, той же стрелкой на циферблате.

Когда нужный момент наступил, сайрес Смит опустился на колени и начал отмечать постепенное уменьшение тени, втыкая в землю маленькие прутики. Товарищи инженера, низко склонившись, с величайшим интересом следили за этой операцией.

Журналист держал в руках свой хронометр, готовясь отметить его показания в ту минуту, когда тень будет всего короче. Вычисление производилось 16 апреля, в день, когда среднее время совпадает с истинным временем. Следовательно, показания часов Гедеона спилета должны были соответствовать истинному вашингтонскому времени, что значительно упрощало вычисления.

Между тем солнце медленно подвигалось по небу. Тень от палочки все короче становилась. Но вот инженеру показалось, что она снова начала удлиняться, и он спросил:

- Который час?

- Пять часов и одна минута, - немедленно ответил спилет.

Теперь оставалось только сделать расчет. Это было весьма просто. Разница во времени между Вашингтоном и островом линкольна составляла, в круглых цифрах, пять часов - иначе говоря, когда на острове линкольна наступил полдень, в Вашингтоне было уже пять часов вечера. Солнце в своем кажущемся движении вокруг земли проходит один градус в четыре минуты, или пятнадцать градусов в час. Пятнадцать градусов, умноженные на пять, составляют семьдесят пять градусов.

Итак, если Вашингтон лежит на 77°3'11", или, в круглых цифрах, на семьдесят седьмом градусе от гринвичского меридиана, который американцы, подобно англичанам, считают за нулевой, то, значит, остров линкольна расположен на 77° 75° к Западу от Гринвича, то есть на 152° западной долготы.

Сайрес смит сообщил эту цифру своим товарищам. Учитывая, как и при измерении широты, погрешности наблюдения, он счел возможным утверждать, что остров линкольна лежит между тридцать пятой и сороковой параллелями и между сто пятидесятым и сто пятьдесят пятым меридианами к Западу от Гринвича.

М - да. Все рассуждения и вычисления безукоризненны, но с практическими наблюдениями на этот раз все совсем плохо. Длина тени около полудня изменяется довольно медленно и определить момент, когда она станет самой короткой вряд ли получится с точностью лучше, чем 10-15 минут, да и наклон гномона "на Глазок", как и возможная негоризонтальность площадки только внесут дополнительные ошибки в измерения. И ведь что самое обидное - инженер ранее определил направление меридиана, но почему-то не воспользовался им для определения момента полдня.

А какова точность полученного нами результата? Попробуем оценить ее хотя бы приблизительно. Примем, что ошибка наблюдения тени гномона в угловой мере не превышает 1/2° и вызвана нечеткостью тени, примерно такую же по величине ошибку могут дать погрешности при установке гномона (отклонение его от вертикали и площадки от горизонтальной поверхности), наши геометрические построения при определении склонения солнца и его высоты - еще 1/2°. То есть суммарная ошибка (а ошибки имеют противное свойство складываться; ) может достигнуть полутора градусов. При определении долготы ошибки вызваны только наблюдениями с помощью гномона, и погрешностью хода наших часов. Лишь в том случае, если мы знаем время с точностью до полуминуты, что составляет 1/8° в переводе в угловые величины, то суммарная ошибка может составить около 1° 8' дуги. Чтобы оценить эти величины в единицах расстояния нужно вспомнить, что 1 морская миля (1852 м) равна средней длине дуги меридиана в 1 угловую минуту. Значит, отклонение определенных нами координат от истинных не превысит 90 миль по широте и 68 миль по долготе, причем с учетом того, что мы находимся не на экваторе (длина дуги в 1' параллели уменьшается с увеличением широты), долготная ошибка может быть заметно меньше.

Координаты звезд. Горизонтальная система координат

Показывает координаты звёзд и других объектов на небесной сфере в режиме «здесь и сейчас» относительно горизонта. Первая координата – это высота объекта над горизонтом. Величина угловая, измеряется в градусах. Максимальное значение +90° (зенит). Нулевое значение координаты имеют светила, расположенные на линии горизонта. И наконец, минимальное значение высоты -90° имеют объекты, находящиеся в точке надира или у наблюдателя «под ногами» - зенит наоборот.

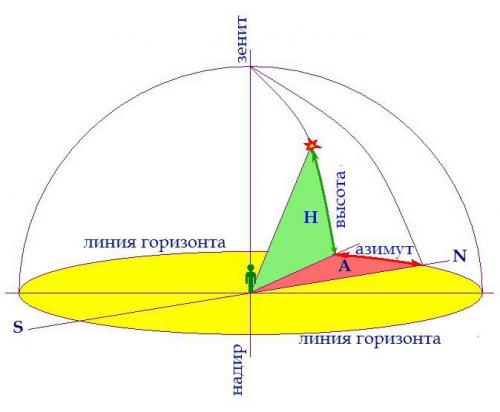
Второй координатой служит азимут − угол между горизонтальными линиями, направленными на объект и на север. Ещё эту систему называют топоцентрической из-за привязки координат к определённой точке на земном шаре.

Система не лишена недостатков. Обе координаты каждой звезды в ней меняются ежесекундно. Поэтому она мало подходит для описания, скажем, расположения звёзд в созвездиях.

Какое склонение-положительное или отрицательное-имеют звезды. Склонение (астрономия)

Экваториальная система координат

Склонение ( δ ) в астрономии  — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах , минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу от него.

• Объект на небесном экваторе имеет склонение 0°
• Склонение северного полюса небесной сферы равно +90°
• Склонение южного полюса равно −90°

У склонения всегда указывается знак, даже если оно положительно.

Склонение небесного объекта, проходящего через зенит , равно широте наблюдателя (если считать северную широту со знаком +, а южную со знаком −).

В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > 90° − φ не заходят за горизонт, поэтому называются незаходящими . Если же склонение объекта δ В южном полушарии Земли незаходящими являются небесные объекты со склонением δ 90° + φ (φ для южного полушария берётся со знаком минус).

Координаты звезд таблица. Координаты Солнца

Суточное изменение склонения Солнца d®в течение месяца до и после дней весеннего и осеннего равноденствия равно 0,4°, в течение месяца до и после дней летнего и зимнего солнцестояний — 0,1°, в течение второго месяца после дней 21.03, 22.06, 23.09, и 22.12—0,3°.Суточное изменение прямого восхождения Солнца a®в течение всего года 1°.Точные значения координат на любой момент выбирают из Морского астрономического ежегодника (МАЕ).С помощью приведенных данных можно найти приближенную меридиональную высоту H ®Солнца на данную дату в широте судна. Для этого рассчитываем на заданную дату d®, затем находим

Например, 25 декабря d®= 23,2° S. В широте (f = 45,5° N; Z® = 45,5° — (— 23,2°) = 68,7°;  H ® = 21,3°.Легко найти и даты начала и конца полярного дня и ночи. Приближенно условием начала и конца полярного дня принимают d®= 90° — (f + 1°) при d®одноименном с f, а условием начала и конца полярной ночи f®= 90°— (f—1°), при f®разноименном с f.Изменение f на 1° приближенно учитывает полудиаметр Солнца и астрономическую рефракцию.Например, в широте 75°N полярный день наступит и закончится при d®== 14° N, т. е. соответственно 1 мая и 13 августа, а полярная ночь будет длиться с 7 ноября до 5 февраля.

Что такое Полярная звезда определение. Описание

См. также: Поляриссима

Полярная звезда и её компаньоны. Снимок Космического телескопа «Хаббл»

В настоящую эпоху Полярная находится менее чем в 1° от Северного полюса мира, и поэтому почти неподвижна при суточном вращении звёздного неба. Она очень удобна для ориентирования: направление на неё практически совпадает с направлением на север , а высота над горизонтом равна географической широте места наблюдения. Из-за прецессии земной оси положение Северного полюса мира меняется; ближе всего Полярная звезда подойдёт к нему в период с 7 марта по 13 июня 2102 года — на расстояние 0°27′34,1″, то есть склонение составит 89°32′25,9″, после чего начнётся её удаление от полюса: к середине 2260 года расстояние от неё до полюса превысит 1°. В южном полушарии нет яркой полярной звезды.

Полярная звезда является ярчайшей и ближайшей к Земле пульсирующей переменной звездой типа дельта Цефея с периодом 3,97 дня. Но Полярная звезда — очень нестандартная цефеида : её пульсации затухают за время порядка десятков лет: в 1900 изменение яркости составляло ±8 %, а в 2005 году  — приблизительно 2 %. Кроме того, за это время звезда стала в среднем на 15 % ярче.

Полярная звезда на самом деле представляет собой тройную звёздную систему. В центре системы располагается сверхгигант Полярная А (α UMi A), превосходящий наше Солнце по яркости в 2000 раз и по массе в 4,5 раза. Полярная B (α UMi B) массой 1,39 массы Солнца расположена на приличном удалении от Полярной А, поэтому разглядеть её в телескопы нетрудно даже с поверхности Земли. В 1929 году при изучении спектра Полярной было выявлено, что Альфа Малой Медведицы является близкой двойной звездой, что было предсказано более ранними наблюдениями в 1924 году (Moore, J.H and Kholodovsky, E. A.). Компаньон Полярной A находится в 18,5 а. е. Полярная P (α UMi P или α UMi a, или α UMi Ab) обладает массой 1,26 массы Солнца и располагается к сверхгиганту настолько близко, что сфотографировать его удалось лишь телескопу « Хаббл », и то лишь после перенастройки оборудования. Приблизительный период обращения Полярной P вокруг α UMi A составляет около 30 лет. Полярная B обращается вокруг двойной системы α UMi A/P прибл. за 100 000 лет. Есть ещё также два далёких компонента, получивших обозначение α UMi C и α UMi D , но это гораздо более старые звёзды и физически они не связаны с Полярной звездой.

Отклонение Полярной звезды от точки севера. Особенности Полярной звезды и главные мифы

Прежде чем искать Полярную звезду, стоит разобраться с ее главными свойствами. Это поможет не только быстрее найти ее на звездном небе, где нет надписей с названиями звезд и линий созвездий, но избежать типичных ошибок. А еще среди людей бытуют заблуждение относительно Полярной звезды. Итак, преимущественно ошибаются в следующих вещах:

1. Полярная звезда находится в зените — то есть прямо над головой. Это очевидно не так: как бы она тогда она указывала на север, раз лежит ровно по центру? «Полярной» звезда называется потому, что размещена на небесной сфере ровно над Северным полюсом Земли. К слову, только там ее можно увидеть посередине неба. Чем дальше от полюса — тем ниже к горизонту опускается звезда, пока полностью не скрывается от глаз на экваторе. По этой же причине Полярная звезда не может служить ориентиром в южной половине планеты — там направление определяют по созвездию Южный Крест .

   

   Звезды Малой Медведицы — созвездия, к которому принадлежит Полярная звезда

   Интересный факт: Полярная звезда действительно помогает определить север точнее компаса. Мы уже знаем, что она находится ровно над Северным полюсом планеты. А вот компас указывает на северный магнитный полюс Земли, который несколько отдален от географического и ежегодно смещается на пару километров. Поэтому ближе к северу Полярная звезда становится наиболее точным инструментом для определения координат.

2. Полярная звезда — самая яркая на небе. Если вы заблудитесь и воспользуетесь этим убеждением, то оно будет стоить вам жизни. Увы, сила сияния — звездная величина Полярной звезды — не очень большая; звезда не входит даже в первые десятки самых ярких звезд, довольствуясь скромным 48-м местом. Впрочем, это не усложняет ее поиск. Но если руководствоваться одной лишь яркостью, больше шансов найти Сириус или Вегу , но никак не Полярную звезду.

   Вокруг Полярной звезды находится множество звезд, которые намного ярче

   Но такое положение вещей продлится ненадолго. Земная ось постоянно смещается по кругу, причем очень быстро в космических масштабах — полный оборот происходит приблизительно за 25800 лет. Поэтому Полярная звезда не всегда была полярной, и останется ею ненадолго. Через 13 тысяч лет место на полюсе займет уже упомянутая яркая Вега, тем самым облегчая поиски севера землянам будущего.

3. Полярная звезда всегда находится на одном и том же месте. Отчасти это правда. Как вы уже наверняка знаете, небесная сфера постоянно вращается — точнее, сама Земля вращается относительно неподвижных звезд. Полярная звезда находится ближе всего к полюсу, и поэтому почти не перемещается. «Почти» тут ключевое слово — отклонение от полюса составляет всего 1°, делая ее наименее подвижной среди других звезд.Однако мы уже знаем, что местоположение Полярной звезды меняется в зависимости от широты. Поэтому в Москве звезду не найти на том месте, где она была вчера Санкт-Петербурге — звезда опустится ниже, ближе к горизонту.Так что единожды найдя Полярную звезду, не стоит расслабляться. В зависимости от сезона, времени суток и географических координат созвездия вокруг занимают разные позиции. Поэтому стоит отработать методику самостоятельного поиска Полярной звезды — тем более что это совсем несложно.

Как найти экваториальные координаты. Экваториальные координаты

Экваториальная система координат  — одна из. В этой системе основной плоскостью является плоскость. Одной из координат при этом является склонение δ (реже — полярное расстояние p ).

Другой координатой может быть:

• часовой угол t (в первой экваториальной системе координат)
• прямое восхождение (во второй экваториальной системе координат)

Первая экваториальная система координат

• Склонением δ светила называется дуга небесного меридиана от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило.

Склонение измеряют в пределах от 0 ° до 90 ° в сторонуи от 0 ° до −90 ° в сторону.

• Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол междуи направлением на светило.

Полярные расстояния измеряют в пределах от 0 ° до 180 ° по направлению от северного полюса мира к южному.

• Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с) до круга склонения светила, илимежду плоскостью небесного меридиана и кругом склонения светила.

Часовые углы отсчитывают в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0 ° до 360 ° (в градусной мере) или от 0чдо 24ч(в часовой мере). Иногда часовые углы измеряют в пределах от 0 ° до 180 ° (от 0чдо 12ч) к западу и от 0 ° до −180 ° (от 0чдо −12ч) к востоку.

Вторая экваториальная система координат

В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной из координат при этом является(δ) (реже — полярное расстояние p). Но вторая координата —(α) — дуга небесного экватора от точки весеннегодо круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Таким образом, начало отсчёта находится в точке, где Солнце пересекаетвесной (точка весеннего равноденствия). Этот угол измеряется к востоку от видимого положения центра Солнца, то есть в сторону, противоположнуювращению небесной сферы, вдоль небесного экватора и принимает значения от 0 ° до 360 ° (в градусной мере) либо от 0чдо 24ч(в часовой мере).

Общие характеристики

• Склонение измеряется в,и. Положительное направление — к северу от небесного экватора, отрицательное — к югу. При склонениях следует указывать знак .
• Объект на небесном экваторе имеет склонение 0 °
• Склонение северного полюса небесной сферы равно +90 °
• Склонение южного полюса равно −90 °
• Склонение небесного объекта, который проходит через, равно

В Северном полушарии Земли для заданной широты φ:

• 
  
• 
  

Поскольку расположение плоскостивследствиепостепенно изменяется, то для экваториальной системы координат всегда указывают, которая определяет некоторое расположение основной плоскости и, соответственно, направление на точку весеннего равноденствия.

Экваториальные координаты звезд таблица. Экваториальные координаты и Звездная карта

Для нахождения звезд на небе, составления звездных карт, для определения времени и географических координат необходимо знать координаты звезд.

Для этого пользуются системой экваториальных координат, которая сходна с системой географических координат на земном шаре.(см. Рисунок 38) Мы можем отсчитывать в градусах положения звезд на небесной сфере относительно небесного экватора так же, как мы отсчитываем угловые расстояния городов от земного экватора на глобусе или на карте ( это расстояние называется географической широтой ). Угловое расстояние светил от небесного экватора называют склонением. Склонения, обозначаемые буквой Дельта, в южном полушарии небесной сферы считаются отрицательными.

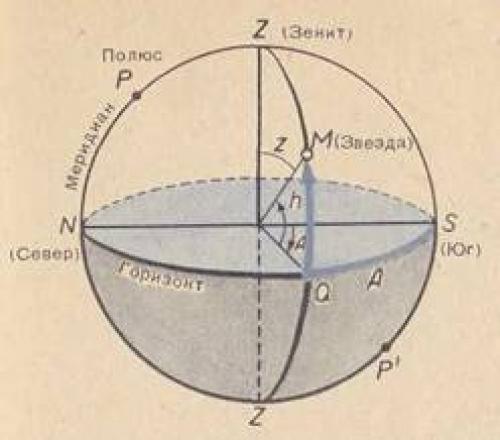
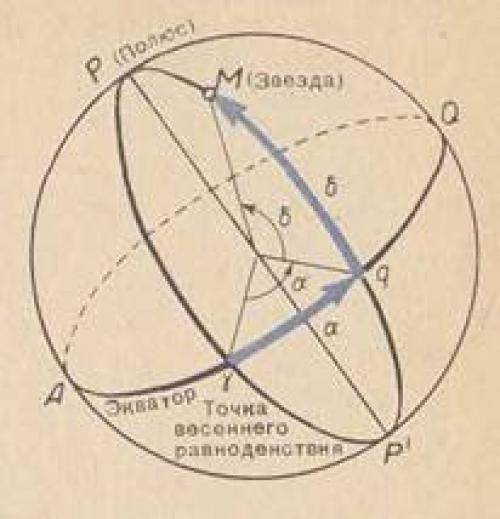
Рисунок 38 - Системы координат. Слева - по отношению к горизонту; высота h и азимут A; справа - по отношению к небесному экватору: прямое восхождение Альфа и склонение Дельта.

Второй географической координатой на Земле является долгота - угол между плоскостью меридиана данного места и плоскостью начального меридиана. На небесной сфере второй координатой является прямое восхождение - угол между плоскостью полукруга, проведенного из полюса мира через светило (круга склонения), и плоскостью полукруга, проведенного из полюса мира через лежащую на экваторе точку весеннего равноденствия (начального круга склонения). Так назвали эту точку потому, что в ней Солнце бывает на небесной сфере 21 марта, когда день равен ночи. Прямое восхождение, обозначаемое Альфа, отсчитывается от точки весеннего равноденствия против часовой стрелки, то есть навстречу суточному вращению неба. Как географическую долготу, так и прямое восхождение удобно выражать не в градусах, а в единицах времени, пользуясь тем, что за 24 часа Земля и, как нам кажется, небо делают один оборот вокруг оси. Отсюда получается соотношение:

Например, географическая долгота, или прямое восхождение, 3 ч 10 мин 20 сек составляет 47°35'00". Легко понять, что звезды кульминируют друг за другом в порядке возрастания их прямого восхождения.

Склонение и прямое восхождение (Альфа и Дельта) называются экваториальными координатами и для звезд меняются так медленно, что их мы можем считать неизменными, если нам не нужна особая точность. При суточном вращении звездного неба вместе с ним вращается и точка весеннего равноденствия. Поэтому положения звезд относительно экватора и точки весеннего равноденствия не зависят ни от времени суток, ни от положения наблюдателя на Земле. В приложении IV дан список координат Альфа и Дельта некоторых ярких звезд. Эта же самая координатная сетка изображена на подвижной карте звездного неба. Солнце, Луна и планеты все время перемещаются на фоне звезд. Поэтому на карте они не помещены (их координаты на каждый день года печатаются в специальных астрономических календарях).