Умножение методом решетки. Решетчатое умножение.

13.09.2016 в 18:28

Содержание

Умножение методом решетки. Решетчатое умножение.
Умножение методом решетки. Умножение чисел
Умножение методом Карацубы. Алгоритм Карацубы. Быстрое умножение.
Умножение методом Ферроля. 2. Умножение методом Ферроля

Похожие презентации

Умножение методом Гаусса. Определение и описание метода Гаусса
Японский метод умножения. Рисуем
Умножение методом бабочки. 16 математических трюков, которые облегчат учебу школьнику

Умножение методом решетки. Решетчатое умножение.

Чтобы освоить умножение многозначных чисел, нужно всего лишь знать таблицу умножения и уметь складывать числа.

В сущности, вся сложность заключается в том, как правильно разместить промежуточные результаты умножения (частичные произведения. Стремясь облегчить вычисления, люди придумали множество способов умножения чисел. За многовековую историю математики их набралось несколько десятков.

Наследие индусов - способ решётки.

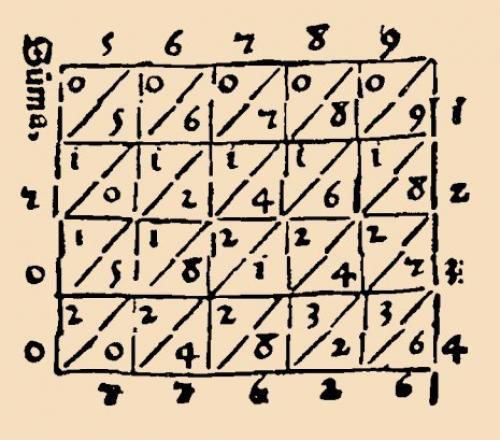Индусы, с давних времён знавшие десятичную систему счисления, пред почитали устный счёт письменному. Они изобрели несколько способов быстрого умножения. Позже их заимствовали арабы, а от них эти способы перешли к европейцам. Те, однако, ими не ограничились и разработали новые, в частности тот, что изучается в школе, - умножение столбиком. Этот способ известен с начала XV века, в следующем столетии он прочно вошёл в употребление у математиков, а сегодня им пользуются повсеместно. Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже, например способ решётки.

Этим способом пользовались ещё в древности, в средние века он широко распространился на Востоке, а в эпоху возрождения - в Европе. Способ решётки именовали также индийским, мусульманским или "Умножением в Клеточку". А в Италии его называли "Джелозия", или "решётчатое умножение" (Gelosia в переводе с итальянского - "жалюзи", "решётчатые ставни". Действительно, получавшиеся при умножении фигуры из чисел имели сходство со ставнями - жалюзи, которые закрывали от солнца окна венецианских домов.

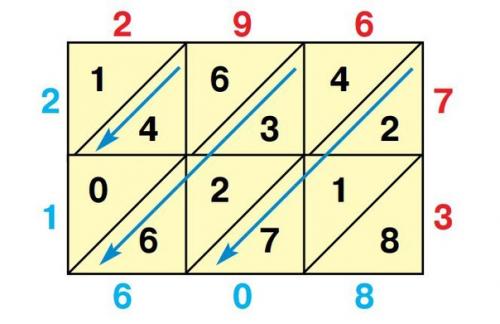
Суть этого нехитрого способа умножения поясним на примере: мы вычислим произведение 296 x 73. Начнём с того, что нарисуем таблицу с квадратными клетками, в которой будет три столбца и две строки, - по количеству цифр в множителях. Клетки пополам по диагонали разделим. Над таблицей запишем число 296, а с правой стороны вертикально - число 73. Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого произведения сложением цифр в косых полосах получим. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 1 7 и т. д. запишем результаты под таблицей, а также слева от неё. В том случае, если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы. Ответ: 21 608. Итак, 296 x 73 = 21 608.

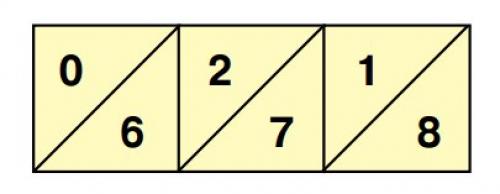Способ решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее, при том, что количество выполняемых действий в обоих случаях одинаково. Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.

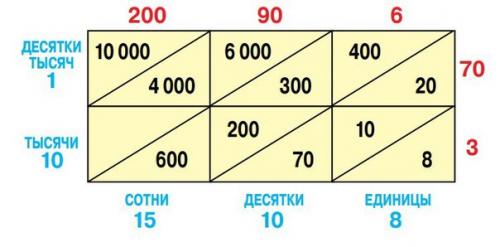
Почему способ решётки приводит к правильному ответу? В чём заключается его "Механизм"? Разберёмся в этом с помощью таблицы, построенной аналогично первой, только в этом случае множители представлены как суммы 200 90 6 и 70 3.

Как видим, в первой косой полосе стоят единицы, во второй - десятки, в третьей - сотни и т. д. при сложении они дают в ответе соответственно число единиц, десятков, сотен и т. д. дальнейшее очевидно:

10 10 1500. 100. 8 _ 21608.

Иначе говоря, в соответствии с законами арифметики произведение чисел 296 и 73 вычисляется так:

296 x 73 = (200 90 6) x (70 3) = 14 000 6300 420 600 270 18 = 10 000 (4000 6000) (300 400 600 200) (70 20 10) 8 = 21 608.

Палочки непера.

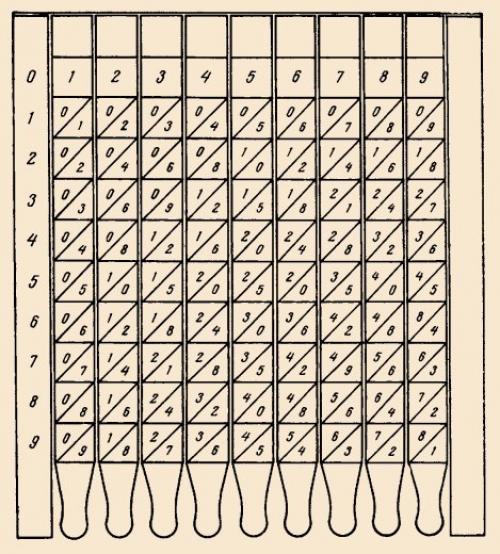
Умножение способом решётки лежит в основе простого и оригинального счётного прибора - палочек непера.

Его изобретатель Джон непер, шотландский барон и любитель математики, наряду с профессионалами занимался усовершенствованием средств и методов вычисления. В истории науки он известен, прежде всего, как один из создателей логарифмов.

Прибор состоит из десяти линеек, на которых размещена таблица умножения. В каждой клетке, разделённой диагональю, записано произведение двух однозначных чисел от 1 до 9: в верхней части указано число десятков, в нижней - число единиц. Одна линейка (левая) неподвижна, остальные можно переставлять с места на место, выкладывая нужную числовую комбинацию. При помощи палочек непера легко умножать многозначные числа, сводя эту операцию к сложению.

Например, чтобы вычислить произведение чисел 296 и 73, нужно умножить 296 на 3 и на 70 (сначала на 7, затем на 10) и сложить полученные числа. Приложим к неподвижной линейке три другие - с цифрами 2, 9 и 6 наверху (они должны образовать число 296. Теперь заглянем в третью строку (номера строк указаны на крайней линейке. Цифры в ней уже знакомый нам набор образуют.

Складывая их, как в способе решётки, получим 296 x 3 = 888. Аналогично, ра? 6

Умножение методом решетки. Умножение чисел

В школе изучают таблицу умножения, а затем учат детей умножать числа в столбик. Разумеется, это не единственный способ умножения. На самом деле, существовало несколько десятков способов умножения и деления многозначных чисел. Приведу здесь, возможно, даже более простой “метод решетки” (см. книгу И.Я. Депман, Н.Я. Виленкин “За страницами учебника математики ”). Рассмотрим этот метод на примере.

Пусть нужно умножитьна. Начертим таблицу, как на рисунке а), запишем над ней числослева направо, а справа от нее — числосверху вниз. В каждую клеточку запишем произведение цифр, стоящих над этой клеточкой и справа от нее. При этом цифру десятков произведения напишем над косой чертой, а цифру единиц — под ней. А теперь будем складывать цифры в каждой косой полосе, показанные на рисунке, выполняя эту операцию справа налево. Если сумма окажется меньше, то ее пишут под нижней цифрой полосы. Если же она окажется больше, то пишут только цифру единиц суммы, а цифру десятков прибавляют к следующей сумме. В результате получаем нужное произведение, которое равно.

Этот способ умножения раньше был распространен на Востоке и в Италии. Чтобы понять его смысл, посмотрим на рисунок б). Видим, что в первой полосе стоят единицы, во второй — десятки, в третьей — сотни и т.д. Иными словами, произведениевычисляется следующим образом:

Есть еще некоторые правила, помогающие быстрому счету. Так, чтобы возвести в квадрат двузначное число, оканчивающееся на, нужно к первой цифре прибавитьи умножить полученное число на эту цифру, а потом к полученному результату приписать. Например, возведем в квадрат. Первая цифра этого числа, прибавим:. Умножимна, получим, дальше просто припишем. Итак, ответ:.

Такое правило следует сразу же из того, что

Разумеется, так можно возводить в квадрат и трехзначные числа, оканчивающиеся на, и числа, которые имеют еще больше знаков. Однако в этих случаях придется вычислять произведение, где в числеуже несколько десятичных знаков, а это тоже приходится делать, скажем, в столбик, то есть это уже сложнее!

Умножение методом Карацубы. Алгоритм Карацубы. Быстрое умножение.

Анатолий Карацуба

Для решения задач современной криптографии необходимы механизмы, реализующие математические операции с большими числами. Чем быстрее будут выполняться эти операции, тем лучше. В качестве курсовой работы по криптографии на 3-м курсе выбрал исследование алгоритма Карацубы. Самое страшное, что на то, чтобы отыскать "в чем фишка" ушло довольно длительное время поиска по просторам интернета… Потом написал код, провел некоторые сравнительные тесты… Но это все уже не так важно и интересно.

В данном топике изложу, как можно проще, суть метода быстрого умножения Карацубы и постараюсь объяснить, чем он лучше.

name='more'>

Для начала рассмотрим, как выполняется обычное умножение "столбиком". Пусть необходимо перемножить числа X и Y . Представим их в виде:

X = aT + b
Y = cT + d

T - можно рассматривать, как "отступ" от "конца" числа или величину сдвига (сколько нулей нужно добавить в конце числа). Т.е. если мы говорим о десятичной системе исчисления, то T - некоторая степень 10-ти. Для простоты возьмем двузначные числа:

X = 12 = 10 + 2
Y = 34 = 30 + 4

Умножение "в столбик" будет выглядеть следующим образом:

XY = (aT + b)(cT + d) = acT2+ (ad + bc)T + bd

Таким образом мы выполняем 4 операции умножения. Для числе из нашего примера:

XY = acT2+ (ad + bc)T + bd = 1х3х102+ (1x4 + 2x3)x10 + 2x4 = 300 + 100 + 8 = 408

Теперь рассмотрим умножение методом Карацубы:

XY = acT2+ (ad + bc)T + bd = acT2+ ((a+b)(c+d) - ac - bd)T + bd

Заметим, что выполняются три операции умножения, вместо четырех. Таким образом сложность вычислений снижается с N2до Nlog(3). (Имеется ввиду двоичный логарифм).

Для чисел из примера:

XY = acT2+ ((a+b)(c+d) - ac - bd)T + bd = 1х3х102+((1 + 2)(3 +4) - 1x3 - 2x4)x10 + 2x4 = 300 + (3x7 - 3 - 8)x10 + 8 = 300 + 100 + 8 = 408

Естественно, для числе малой разрядности метод Карацубы выглядит более громоздким и неудобным. Более того, для менее чем 32-разрядных (на 32-разрядной архитектуре) и менее 64-х разрядных (на 64-разрядной архитектуре) метод Карацубы, согласно моим опытам, проигрывает во времени умножению "в столбик". Но после этого порога наблюдается обратная тенденция. А с учетом того, что результаты разложения чисел, мы также можем перемножать методом Карацубы (до тех пор, пока их разрядность не опустится ниже разрядности архитектуры), то при переходе разрядности чисел в следующую степень двойки мы получаем скачок в разности скорости работы алгоритмов.

Умножение методом Ферроля. 2. Умножение методом Ферроля

2. Умножение методом Ферроля. Для умножения единиц произведения переумножения перемножают единицы множителей, для получения десятков, умножают десятки одного на единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроля легко перемножать устно двухзначные числа от 10 до 20. Например: 12х14=. 1. 6. 8. А)2х4=8, пишем 8. Б)1х4+2х1=6, пишем 6. В)1х1=1, пишем 1.

Слайд 10 из презентации «Cтаринные способы умножения»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как…». Скачать всю презентацию «Cтаринные способы умножения.pptx» можно в zip-архиве размером 364 КБ.

Умножение методом Гаусса. Определение и описание метода Гаусса

Метод преобразований Гаусса (также известный как преобразование методом последовательного исключения неизвестных переменных из уравнения или матрицы) для решения систем линейных уравнений представляет собой классический методом решения системы алгебраических уравнений (СЛАУ). Также этот классический метод используют для решения таких задач как получение обратных матриц и определения ранговости матрицы.

Преобразование с помощью метода Гаусса заключается в совершении небольших (элементарных) последовательных изменениях системы линейных алгебраических уравнений, приводящих к исключению переменных из неё сверху вниз с образованием новой треугольной системы уравнений, являющейся равносильной исходной.

Определение 1

Эта часть решения носит название прямого хода решения Гаусса, так как весь процесс осуществляется сверху вниз.

После приведения исходной системы уравнений к треугольной осуществляется нахождение всех переменных системы снизу вверх (то есть первые найденные переменные занимают находятся именно на последних строчках системы или матрицы). Эта часть решения известна также как обратный ход решения методом Гаусса. Заключается его алгоритм в следующем: сначала вычисляется переменные, находящиеся ближе всего к низу системы уравнений или матрицы, затем полученные значения подставляются выше и таким образом находится ещё одна переменная и так далее.

Японский метод умножения. Рисуем

Это удивительно, но японские дети умеют умножать большие числа, даже не зная о таблице умножения. Как умножают японцы? Они делают это очень просто, настолько просто, что используют лишь базовые навыки рисования и счета. Проще показать на примере, как это происходит.

Допустим, необходимо умножить 123 на 321. Для начала нужно нарисовать одну, две и три параллельные линии, которые будут размещаться по диагонали с верхнего левого угла в нижний правый. На созданных группах параллелей нарисовать три, две и одну линию соответственно. Они также будут размещаться по диагонали с нижнего левого угла в правый верхний.

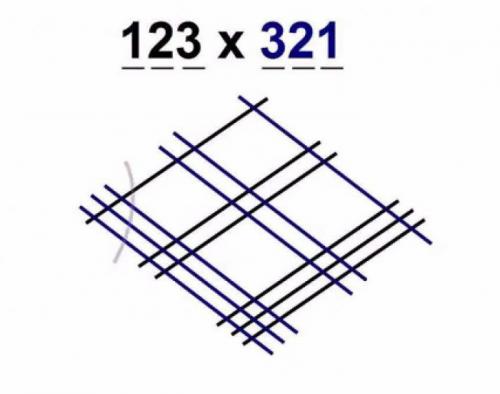
В итоге получим так называемый ромб (как на рисунке выше). Если кто еще не понял, количество линий в группе зависит от чисел, которые нужно перемножить.

Умножение методом бабочки. 16 математических трюков, которые облегчат учебу школьнику

Ребенок приносит плохие оценки по математике, не любит считать и с боем в начальных классах учил таблицу умножения? Возможно, это «не его» предмет, но даже гуманитарий может полюбить математику благодаря простым математическим трюкам.

Математические трюки помогут школьникам с первого и по одиннадцатый класс. Простые математические приемы научат, как делить на 6, вспомнить число Пи, найти процент от числа, выучить таблицу умножения и решат много других вопросов. Мы выбрали 16 трюков, которые облегчат уроки математики школьнику и могут пригодиться родителям.

Процент от числа

Быстрое возведение в квадрат

Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножьте первую цифру саму на себя + 1, а в конце допишите 25.

Умножение на 4

Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2.

Умножение на 5

Разделите число на 2. Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.

Таблица умножения 6, 7, 8, 9 на руках

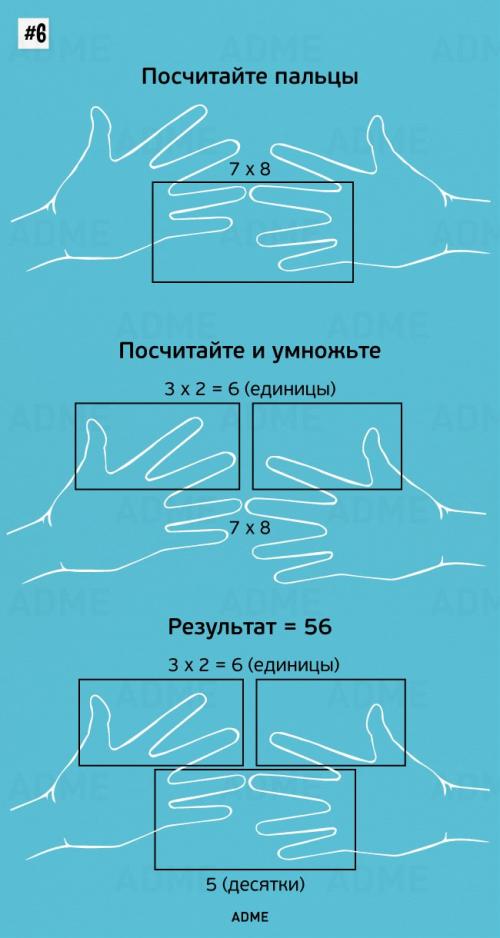
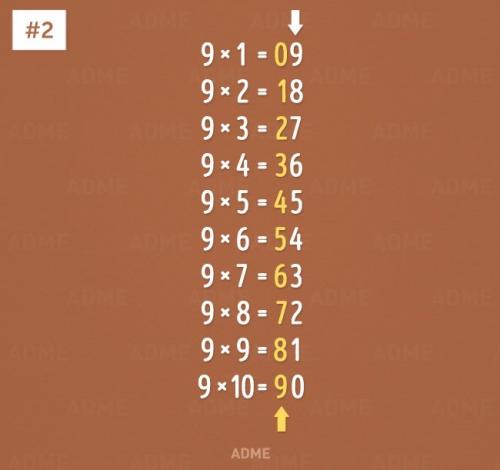
Умножение на 9

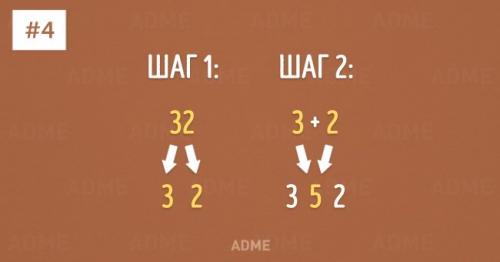
Умножение на 11

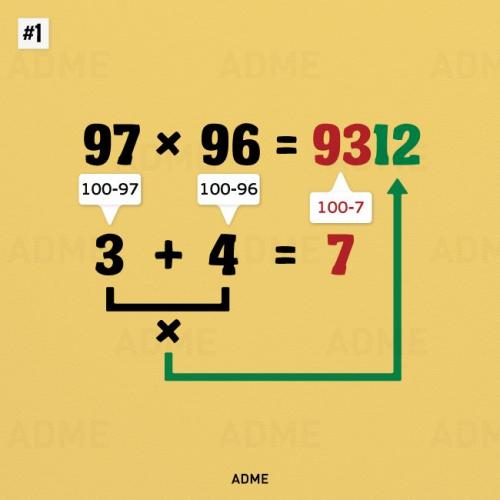
Умножение больших чисел в уме

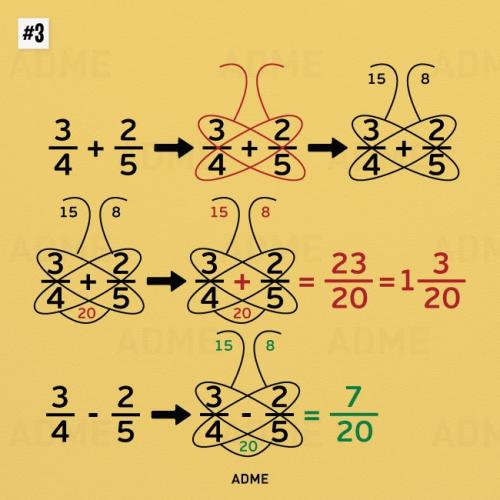
Метод бабочки для сложения и вычитания дробей

Как вспомнить число Пи

Как найти дробь от целого числа

Сложное умножение

Если вам нужно умножить большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ.

Деление на 5

Чтобы разделить большие числа на 5, нужно просто умножить на 2 и перенести запятую.

Вычитание из 1000

Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: отнимите от 9 все цифры, кроме последней, а последнюю цифру отнимите от 10.