Зачем нужны пределы и интегралы и как их "Правильно" понимать?

Прежде чем ответить на первую часть вопроса, стоит разобрать вторую составляющую.
Мы представим, у вам необходимо огородить территорию забором. Ввиду отсутствия опыта в столярном деле, вы нанимаете подрядчика, даете ему необходимы материал (дерево в виде досок. Ходят слухи, что данный подрядчик "Халявит", забирая часть стройматериала себе. На момент завершения работ вы решились проверить, все ли материалы ушли на воздвижение забора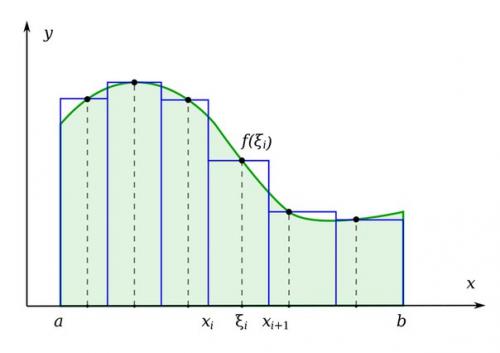
. Заранее условимся, что доски - "Идеальные" - имеют одинаковую толщину. То есть, чтобы найти объем дерева (кубометры), вам необходимо найти площадь поверхности досок, а доски прямоугольные - да что тут, по сути сложного - ширина на высоту.

А теперь частично абстрагируемся от всего этого, представляя, что забор не имеет зазоров и верхушка забора имеет криволинейную форму (описываемую неким уравнением y = f (x), где x - координата длины забора, забор идет строго прямо, без всяких закруглений.
Задача усложняется: не получится точно высчитать площадь. И тут на помощь приходят пределы. Делим этот "Криволинейный" забор на множество прямоугольных дощечек; причем не принципиально делить их на равные длины. Почему? Да потому что достаточно устремить длину самой максимальной доски к нулю (она не достигает нуля, но есть величина близка к нему), что повлечет за собой устремление к нулю всех меньших. А теперь все это "Суммируем", но такая сумма имеет бесконечно много составляющих, поэтому она перетекает в интеграл (собственно, определенный.
Теперь непосредственно к физике.
Из школьного курса известно, что работа отдельной силы (или результирующей систему сил, приложенных к одной материальной точке) по перемещению (важно, вдоль прямой, которую можно связать с координатой x, например) есть скалярное произведение силы (результирующей) на вектор перемещения. В скалярной форме - сила * перемещение * косинус угла между силой и перемещением.
А что если сила в определенной точке координаты имеет разное значение, иными словами, сила - функция от координаты? И как, следовательно, найти работу? И тут также помогает интеграл.