Квантовая запутанность. Червоточины и квантовая запутанность.
- Квантовая запутанность. Червоточины и квантовая запутанность.
- Квантовая запутанность квантовый компьютер. Теорема Белла. Спор разрешён?
- Что такое квантовая запутанность простыми словами. Что мы знаем о квантах и их причудах?
- Квантовая запутанность простыми словами. Квантовая запутанность для чайников
- Квантовая запутанность передача информации. Что получается из квантовой механики
- Видео Квантовая запутанность, суперпозиция и телепортация / Просто о
- Квантовая запутанность на английском. Еще значения слова и перевод КВАНТОВАЯ ЗАПУТАННОСТЬ с английского на русский язык в англо-русских словарях.
- Квантовая запутанность новости. Квантовая запутанность может быть неотъемлемым свойством реальности
Квантовая запутанность. Червоточины и квантовая запутанность.
Червоточины - это гипотетическое свойство вселенной: считается, что с их помощью можно легко попасть в самые далёкие галактики. Они могут существовать благодаря феномену квантовой запутанности - в теории частицы могут быть тесно связаны между собой независимо от разделяющего их расстояния.
Учёные давно работают над теорией, которая могла бы объяснить все свойства космического пространства, от частиц до галактик. В настоящее время исследователи имеют две теории - квантовую механику и общую теорию относительности. Обе теории описывают законы вселенной независимо друг от друга: квантовая теория описывает поведение мельчайших объектов, а теория относительности - крупных объектов. В настоящее время существует также несколько различных теорий, пытающихся объединить все свойства пространства.
Теория относительности, разработанная Альбертом Эйнштейном, включает в себя червоточины, официально известные как мосты Эйнштейна - Розена. Эти деформации пространства - времени могут быть туннелями, соединяющими любые чёрные дыры во вселенной.
Интересно, что в квантовой механике тоже описан подобный феномен - та самая квантовая запутанность, о которой мы уже упоминали. Многочисленные эксперименты доказали, что квантовая запутанность действительно существует, а следовательно, может лечь в основу передовых технологий в будущем вроде мощнейших квантовых компьютеров или сверхзащищённого квантового шифрования.
Физики - теоретики Хуан Мартин малдасена из института перспективных исследований в Принстоне и Леонард сасскинд из стэнфордского университета независимо друг от друга утверждают, что червоточины связаны с запутанностью. В частности, они предположили, что у каждой чёрной дыры есть пара, и обе дыры связаны друг с другом именно благодаря запутанности.
Запутанные чёрные дыры могут возникнуть несколькими способами. Например, обе дыры могут образоваться одновременно и автоматически стать запутанными. Кроме того, частицы, захватываемые одной чёрной дырой, могут "Рухнуть" в другую дыру, что автоматически сделает их запутанными. Малдасена и сасскинд утверждают, что запутанность, возможно, всегда связана с червоточинами: например, мельчайшие частицы, фотоны и электроны, могут быть связаны именно путём микроскопических червоточин.
На первый взгляд такое утверждение может показаться абсурдным. Например, запутанность работает даже тогда, когда сила тяжести не действует. Но учёные исследовали, как запутанные пары частиц ведут себя при теории суперсимметрии, предполагающей, что все известные элементарные частицы имеют "Суперпартнёра".
Считается также, что с помощью подобной квантово - механической теории можно объяснить поведение объектов в четырёх изменениях (четвёртое - время. В случае если же теория червоточин верна, то в дело вступает дополнительное пятое измерение - таким образом, червоточины и запутанность могут быть по сути одним и тем же явлением.
Квантовая запутанность квантовый компьютер. Теорема Белла. Спор разрешён?
Джон Клаузер, будучи ещё аспирантом Колумбийского университета, в 1967 отыскал забытую работу ирландского физика Джона Белла. Это была сенсация: оказывается Беллу удалось вывести из тупика спор Бора и Энштейна . Он предложил экспериментально проверить обе гипотезы. Для этого он предложил построить машину, которая бы создавала и сравнивала много пар запутанных частиц. Джон Клаузер принялся разрабатывать такую машину. Его машина могла создавать тысячи пар запутанных частиц и сравнивать их по разным параметрам. Результаты экспериментов доказывали правоту Бора.
А вскоре французский физик Ален Аспе провёл опыты, один из которых касался самой сути спора между Энштейном и Бором. В этом опыте измерение одной частицы могло прямо повлиять на другую только в случае, если сигнал от 1-й ко 2-й прошёл бы со скоростью, превышающей скорость света. Но сам Энштейн доказал, что это невозможно. Оставалось только одно объяснение – необъяснимая, сверхъестественная связь между частицами.
Результаты опытов доказали, что теоретическое предположение квантовой механики – верно. Квантовая запутанность – это реальность ( ). Квантовые частицы могут быть связанными несмотря на огромные расстояния. Измерение состояния одной частицы влияет на состояние далеко расположенной от нёё 2-й частицы так, как если бы расстояния между ними не существовало. Сверхъестественная связь на расстоянии происходит в действительности.
Что такое квантовая запутанность простыми словами. Что мы знаем о квантах и их причудах?
На сегодня квантовая физика ушла достаточно далеко. Открыто много различных явлений. Но что мы знаем на самом деле? Ответ представлен одним учёным современности. "В квантовую физику можно либо верить, либо ее не понимать", - таково определение Ричарда Фейнмана. Подумайте над этим сами. Достаточно будет упомянуть такое явление, как квантовая запутанность частиц. Это явление ввергло научный мир в положение полного недоумения. Ещё большим шоком стало то, что возникший парадокс несовместим с законами Ньютона и Эйнштейна.
Впервые эффект квантовой запутанности фотонов обсуждался в 1927 году на пятом Солвеевском Конгрессе. Между Нильсом Бором и Эйнштейном возник жаркий спор. Парадокс квантовой спутанности полностью изменил понимание сути материального мира.
Известно, что все тела состоят из элементарных частиц. Соответственно, все явления квантовой механики отражаются в обычном мире. Нильс Бор говорил, что если мы не смотрим на Луну, то её не существует. Эйнштейн считал это неразумным и полагал, что объект существует независимо от наблюдателя.
При изучении проблем квантовой механики следует понимать, что её механизмы и законы взаимосвязаны между собой и не подчиняются классической физике. Попробуем разобраться в самой противоречивой области – квантовой запутанности частиц.
Квантовая запутанность простыми словами. Квантовая запутанность для чайников
В обсужденияхя заметил несколько сообщений, от людей, которые думают, что «физики договорились» о существовании суперпозиции. Что это просто удобная математическая/физическая модель, не имеющая под собой реальных экспериментов, доказывающих нахождение квантов в суперпозиции. Что кванты, на самом деле находятся всегда в конкретных позициях, а проведение эксперимента, лишь обнаруживает эти позиции. Некоторое время это было спором и у физиков, пока в 1964 году Джон Стюарт Белл не сформулировал свою известную теорему Белла(неравенства Белла), которая в последствии была улучшена другими учеными и неоднократно проверена экспериментально. Для желающих ознакомиться непосредственно с его теоремой, я советую пропустить эту статью, и сразу перейти к прочтению книг, ссылки на которые даны ниже, и в комментариях. Для понимания ее основ не требуются глубокие познания физики и математики. Для тех же, кому дажекажется сложной для понимания, я приведу довольно упрощенную аналогию.Для простоты, скажем, у кванта есть некоторые 3 характеристики: A, B и C, которые могут принимать значения 1 или 0. Возьмем два запутанных кванта, таких, что:1) Если при измерении у первого кванта одной из характеристик мы получаем 1, то у другого кванта, эта же характеристика при измерении будет равна 0.2) Если мы выбираем для сравнения характеристику случайным образом, то в половине случаев мы получаем одинаковые значения, а в половине — разные. (!)Сперва кажется что выполнить эти два условия очень легко, написав простенькую программу мы можем смоделировать эту ситуацию. НО! Давайте просто проверим это статистически, программно, кто как хочет и может, пусть проведет свое собственное исследование: Поставит такой эксперимент: Создаст N заранее определенных пар троек значений: (1,0,1)-(0,1,0); (1,1,0)-(0,0,1)… итп, далее построит модель, которая будет удовлетворять обоим вышеуказанным пунктам.Окажется, что это не только непросто сделать, но и в принципе невозможно. Если мы с такими исходными данными будем измерять одинаковые параметры, мы будем получать противоположные значения. Что понятно и согласуется с пунктом 1. Но вот если, мы будем измерять случайные параметры, то противоположные значения у нас будут появляться в более чем 50% случаев . Что противоречит пункту 2.
Небольшой кусок кода на С#, с попыткой написать такую модель
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace ConsoleApplication14
{
class Program
{
static void Main(string args)
{
int confirm = 0, notconfirm = 0;
Random rnd = new Random();
List
Квантовая запутанность передача информации. Что получается из квантовой механики
Квантовые частицы может находиться в двух типах состояний, согласно классическому учебнику Ландау и Лифшица — чистом и смешанном. Если частица не взаимодействует с другими квантовыми частицами, она описывается волновой функцией, зависящей только от её координат или импульсов — такое состояние называют чистым. В этом случае волновая функция подчиняется уравнению Шредингера. Возможен другой вариант — частица взаимодействует с другими квантовыми частицами. В этом случае волновая функция относится уже ко всей системе взаимодействующих частиц и зависит от всех их динамических переменных. Если мы интересуемся только одной частицей, то её состояние, как показал Ландау ещё 90 лет назад, можно описать матрицей или оператором плотности. Матрица плотности подчиняется уравнению, аналогичному уравнению Шредингера
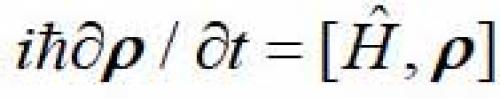где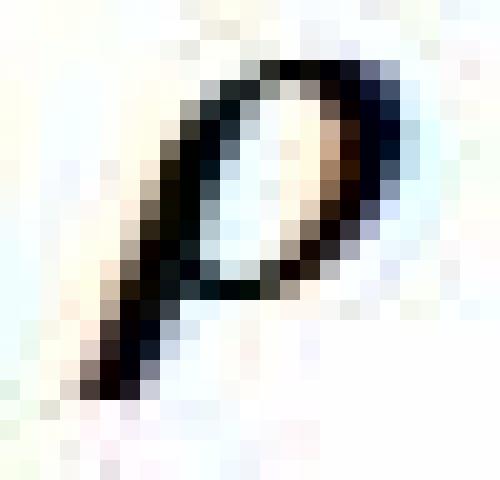
— матрица плотности, H — оператор Гамильтона, а скобки обозначают коммутатор.Его вывел Ландау. Любые физические величины, относящиеся к данной частицы, можно выразить через матрицу плотности. Такое состояние называют смешанным. Если у нас есть система взаимодействующих частиц, то каждая из частиц находится в смешанном состоянии. Если частицы разлетелись на большие расстояния, и взаимодействие исчезло, их состояние все равно останется смешанным. Если же каждая из нескольких частиц находятся в чистом состоянии, то волновая функция такой системы есть произведение волновых функций каждой из частиц (если частицы различны. Для одинаковых частиц, бозонов или фермионов, надо составить симметричную или антисимметричную комбинацию см. , но об этом позже. Тождественность частиц, фермионы и бозоны – это уже релятивистская квантовая теория.Запутанным состоянием пары частиц называется такое состояние, в котором имеется постоянная корреляция между физическими величинами, относящимися к разным частицам. Простой и наиболее часто распространенный пример — сохраняется некая суммарная физическая величина, например, полный спин или момент импульса пары. Пара частиц при этом находится в чистом состоянии, но каждая из частиц — в смешанном. Может показаться, что изменение состояния одной частицы сразу скажется на состоянии другой частицы. Даже если они разлетелись далеко и не взаимодействуют, Именно это высказывается в популярных статьях. Это явление уже окрестили квантовой телепортацией, Некоторые малограмотные журналисты даже утверждают, что изменение происходит мгновенно, то есть распространяется быстрее скорости света.Рассмотрим это с точки зрения квантовой механики, Во-первых, любое воздействие или измерение, меняющее спин или момент импульса только одной частицы, сразу же нарушает закон сохранения суммарной характеристики. Соответствующий оператор не может коммутировать с полным спином или полным моментом импульса. Таким образом, нарушается первоначальная запутанность состояния пары частиц. Спин или момент второй частицы уже нельзя однозначно связать с таковым для первой. Можно рассмотреть эту проблему с другой стороны. После того, как взаимодействие между частицами исчезло, эволюция матрицы плотности каждый из частиц описывается своим уравнением, в которое динамические переменные другой частицы не входят. Поэтому воздействие на одну частицу не будет менять матрицу плотности другой.Имеется даже теорема Эберхарда , которая утверждает, что взаимное влияние двух частиц невозможно обнаружить измерениями. Пусть имеется квантовая система, которая описывается матрицей плотности. И пусть эта система состоит из двух подсистем A и B. Теорема Эберхарда гласит, что никакое измерение наблюдаемых, связанных только с подсистемой A, не влияет на результат измерения любых наблюдаемых, которые связаны только с подсистемой B. Впрочем, доказательство теоремы использует гипотезу редукции волновой функции, которая не доказана ни теоретически, ни экспериментально. Но все эти рассуждения сделаны в рамках нерелятивистской квантовой механики и относятся к различным, не тождественным частицам.Эти рассуждения не работают в релятивистской теории в случае пары одинаковых частиц. Еще раз напомню, что тождественность или неразличимость частиц – из релятивистской квантовой механики, где число частиц не сохраняется. Однако для медленных частиц мы можем использовать более простой аппарат нерелятивистской квантовой механики, просто учитывая неразличимость частиц. Тогда волновая функция пары должна быть симметричной (для бозонов) или антисимметричной (для фермионов) по отношению к перестановке частиц. Такое требование возникает в релятивистской теории, независимо от скоростей частиц. Именно это требование приводит к дальнодействующим корреляциям пары одинаковых частиц. В принципе протон с электроном тоже могут находиться в запутанном состоянии. Однако если они разойдутся на несколько десятков ангстрем, то взаимодействие с электромагнитными полями и другими частицами разрушит это состояние. Обменное взаимодействие (так называют это явление) действует на макроскопических расстояниях, как показывают эксперименты. Пара частиц, даже разойдясь на метры, остается неразличимой. Если вы проводите измерение, то вы точно не знаете, к какой частице относится измеряемая величина. Вы проводите измерения с парой частиц одновременно. Поэтому все эффектные эксперименты проводились именно с одинаковыми частицами – электронами и фотонами. Строго говоря, это не совсем то запутанное состояние, которое рассматривают в рамках нерелятивистской квантовой механики, но что-то похожее.Видео Квантовая запутанность, суперпозиция и телепортация / Просто о
Квантовая запутанность на английском. Еще значения слова и перевод КВАНТОВАЯ ЗАПУТАННОСТЬ с английского на русский язык в англо-русских словарях.
- ЗАПУТАННОСТЬ — f. complexity, intricacy
Russian-English Dictionary of the Mathematical Sciences - ЗАПУТАННОСТЬ — Intricacy
Русско-Американский Английский словарь - ЗАПУТАННОСТЬ — Entanglement
Русско-Американский Английский словарь - ЗАПУТАННОСТЬ — confusion
Англо-Русско-Английский словарь общей лексики - Сборник из лучших словарей - ЗАПУТАННОСТЬ — confusion; ~ый tangled; перен. intricate, involved; ~ый вопрос knotty question; оказаться ~ым в чем-л. become* involved in smth complexity, complication, …
Русско-Английский словарь общей тематики - ЗАПУТАННОСТЬ — ж. confusion
Русско-Английский словарь - ЗАПУТАННОСТЬ — ж. confusion
Russian-English Smirnitsky abbreviations dictionary - ЗАПУТАННОСТЬ — Tangle
Британский Русско-Английский словарь - ЗАПУТАННОСТЬ — Imbroglio
Британский Русско-Английский словарь - ЗАПУТАННОСТЬ — Entanglement
Британский Русско-Английский словарь - ЗАПУТАННОСТЬ — Complication
Британский Русско-Английский словарь - ЗАПУТАННОСТЬ — confusion; ~ый tangled; перен. intricate, involved; ~ый вопрос knotty question; оказаться ~ым в чем-л. become* involved in smth
Русско-Английский словарь - QD - КВАНТОВАЯ — фундаментальная физическая теория динамического поведения всех элементарных форм вещества и излучения, а также их взаимодействий. Квантовая механика представляет собой теоретическую …
Русский словарь Colier - ЗАПУТАННОСТЬ — жен. complexity, complication, inextricably, intricacy, plexus запутанн|ость - ж. confusion ~ый tangled перен. intricate, involved ~ый вопрос knotty question оказаться …
Большой Русско-Английский словарь - ЗАПУТАННОСТЬ — запутанность embroilment
Русско-Английский словарь Сократ - КВАНТОВЫЙ — adj. quantum; квантовая теория, quantum theory; квантовая механика, quantum mechanics
Russian-English Dictionary of the Mathematical Sciences - WAVE — 1. сущ. 1) вал, волна the waves поэт. ≈ море the sound of the waves breaking on the shore ≈ …
Большой Англо-Русский словарь - QW — сокр.
Квантовая запутанность новости. Квантовая запутанность может быть неотъемлемым свойством реальности
Действительно ли явление под названием квантовая запутанность необходимо для описания физического мира или же возможна некая пост-квантовая теория без запутанности? В новом исследовании, о котором пишет phys.org, физики математически доказали, что любая теория с классическим пределом – когда она может описывать наши наблюдения классического мира, обращаясь к классической теории при определенных условиях – должна включать запутанность. Поэтому, несмотря на то, что запутанность расходится с классическим пониманием, она должна быть неизбежным и важнейшим свойством не только квантовой теории, но и любой неклассической теории, даже еще не разработанной.
Физики в лице Джонатана Риченса из Имперского колледжа Лондона и Университетского колледжа Лондона, Джона Селби из Имперского колледжа Лондона и Оксфордского университета и Сабри Аль-Сафи из Университета Ноттингем-Трент, опубликовали статью, в которой говорится о том, что запутанность является неизбежной особенностью любой неклассической теории, в Physical Review Letters.
«У квантовой теории много странных особенностей по сравнению с классической теорией», говорит Риченс. «По традиции мы изучаем, как классический мир выходит из квантового, но тут мы решили обратить вспять это рассуждение, чтобы увидеть, как классический мир формирует квантовый. Так мы показали, что одна из самых странных особенностей последнего, квантовая запутанность, является неизбежным следствием выхода за рамки классической теории или, возможно, даже следствием нашей неспособности отказаться от классической теории, оставить ее позади».
Хотя полное доказательство намного подробнее, основная идея заключается в том, что любая теория, описывающая реальность, должна вести себя как классическая теория в некотором пределе. Это требование кажется довольно очевидным, но, как показывают физики, оно накладывает серьезные ограничения на структуру любой неклассической теории.
Квантовая теория удовлетворяет этому требованию наличия классического предела в процессе декогеренции. Когда квантовая система взаимодействует с внешней средой, она теряет свою квантовую когеренцию, связанность, и все, что делает ее квантовой. Таким образом, система становится классической и ведет себя как, как ожидается в классической теории.
Физики показали, что любая неклассическая теория, которая восстанавливает классическую теорию, должна содержать запутанные состояния. Чтобы доказать это, они пошли от обратного: допустим, такая теория не имеет запутанности. И затем они показали, что без запутанности любая теория, которая восстанавливает классическую теорию, должна быть сама классической – и это противоречит изначальной гипотезе, что такая теория должна быть неклассической. Этот результат означает, что предположение отсутствия запутанности в такой теории будет ложным, а значит, любая теория такого типа должна ее иметь.
Этот результат может быть только началом многих других связанных открытий, поскольку открывает возможность того, что другие физические особенности квантовой теории можно воспроизвести, просто потребовав от теории наличия классического предела. Физики предполагают, что такие особенности, как информационная каузальность (причинно-следственная связь), битовая симметрия и макроскопическая локальность могут быть доказаны, благодаря этому единственному требованию. Эти результаты также дают более четкое представление о том, как должна выглядеть любая будущая неклассическая, постквантовая теория.
«Мои будущие цели состоят в том, чтобы увидеть, может ли нелокальность Белла также извлечена из существования классического предела», говорит Риченс. «Было бы интересно, если бы все теории, заменяющие классическую теорию, нарушали бы локальный реализм».
Локальный реализм — это комбинация принципа локальности с «реалистичным» предположением, что все объекты обладают «объективно существующими» значениями своих параметров и характеристик для любых возможных измерений, могущих быть произведенными над этими объектами, перед тем как эти измерения производятся. Эйнштейн, будучи, по всей видимости, сторонником локального реализма, любил в связи с этим говорить, что Луна не исчезает с неба, даже если её никто не наблюдает. Данные современной квантовой механики, основанные на проведенных экспериментах, ставят под сомнение адекватность модели локального реализма «устройству» реальности.