Опыт Юнга может перевернуть наше представление о реальности.

Опыт Юнга может перевернуть наше представление о реальности.

Традиционный эксперимент в области физики может скрывать в себе знания о природе реальности, о которых мы и не догадывались. Классический опыт юнга, известный также как "Эксперимент на Двух Щелях", в свое время стал доказательством волновой теории света. Но на самом деле он бросает вызов одному из самых известных и изученных предположений квантовой механики.

Суть эксперимента заключается в том, что на непрозрачный экран - ширму с двумя параллельными прорезями, позади которого установлен другой, проекционный экран, направляют пучок света. Особенность прорезей заключается в том, что их ширина приблизительно равна длине волны излучаемого света. Логично было бы предположить, что фотоны должны проходить сквозь щели, создавая две параллельные полосы света на заднем экране. Но вместо этого свет распространяется в виде полос, в которых чередуются участки света и темноты, то есть свет ведет себя как волна. Это явление называется "Интерференция", и именно его демонстрация Томасом Юнгом стала доказательством справедливости волновой теории. Переосмысление этого эксперимента могло бы объединить квантовую механику с другой опорой теоретической физики, общей теорией относительности энштейна, - вызов, который до сих пор остается неразрешимым на практике.

Для того, чтобы вычислить вероятность появления фотона в том или ином месте на экране, физики используют принцип под названием "Правило Борна". Тем не менее, для этого нет никаких причин - эксперимент всегда проходит одинаково, но никто не знает почему. Некоторые энтузиасты пытались объяснить этот феномен из интерпретации квантово - механической теории о "Множественных Мирах", в которой предполагается, что все возможные состояния квантовой системы могут существовать в параллельных вселенных, но эти попытки ни к чему не привели.
Это обстоятельство позволяет использовать правило Борна как доказательство наличия в квантовой теории нестыковок. Для того, чтобы объединить квантовую механику, которая оперирует вселенной в узких временных масштабах, и общую теорию относительности, которая работает с огромными промежутками времени, одна из теорий должна уступить дорогу. Только в том случае, если же правило Борна неверно, то это будет первый шаг к изучению квантовой гравитации. "Если Правило Борна Будет Нарушено, что Будет Нарушена и Фундаментальная Аксиома Квантовой Механики, и мы Узнаем, где Следует Искать Ответ на Теории о Квантовой Гравитации", говорит Джеймс куотч из института науки и техники в Испании.
Куотч предложил новый способ проверить правило борна. Он исходил из идеи физика фейнмана: для того, чтобы вычислить вероятность возникновения частицы в той или иной точке экрана, вы должны учитывать все возможные пути, по которым это может произойти, даже если они кажутся смешными. "Учитывается Даже та Вероятность, что Частица Долетит до Луны и Вернется Обратно", говорит куотч. Практически ни один из путей не повлияет на окончательное местоположение фотона, но некоторые, весьма необычные, могут в конечном итоге изменить его координаты. К примеру предположим, что у нас есть три пути, благодаря которым частица может пролететь сквозь экран, вместо двух очевидных (т. е. вместо той или иной щели. Правило Борна в этом случае позволяет рассматривать помехи, которые могут возникнуть между двумя очевидными вариантами, но не между всеми тремя.
Джеймс показал, что, если учитывать все возможные отклонения, то итоговая вероятность того, что фотон угодит в точку Х, будет отличаться от результата, который предполагает правило Борна. Он предложил использовать в качестве третьего пути блуждающий зигзаг: так, частица проходит сначала сквозь левое отверстие, затем сквозь правое, и лишь затем направляется к экрану. Внимание! Только в том случае, если третий путь препятствует первым двум - изменится и результат вычислений. Работа куотча вызвала большой интерес, и анинда синха в индийском институте науки в Бангалоре - член команды, которая впервые предложила использовать для опровержения правила Борна извилистые, "Нетрадиционные" пути, - с ней полностью согласен. Однако ученый указывает и на то, что существует слишком много неучтенных вероятностей, чтобы сейчас можно было говорить о чистоте эксперимента. Как бы то ни было, результаты этой работы откроют человечеству дверь в область более глубокого понимания реальности. Источник: Popmech. ru.

Дисперсия света

Каждый из нас когда-нибудь видел, как переливаются лучи на граненых изделиях из стекла или, например, на бриллиантах. Наблюдать это можно благодаря такому явлению, как дисперсия света. Это эффект, отражающий зависимость показателя преломления предмета (вещества, среды) от длины (частоты) световой волны, которая проходит через этот предмет. Следствием такой зависимости является разложение луча на цветовой спектр, например, при прохождении через призму. Дисперсия света выражается следующим равенством:

n = ƒ (ƛ),

где n – показатель преломления, ƛ – частота, а ƒ – длина волны. Показатель преломления увеличивается с ростом частоты и уменьшением длины волны. Дисперсию мы нередко наблюдаем в природе. Самым красивым ее проявлением является радуга, которая образуется благодаря рассеиванию солнечных лучей при прохождении их через многочисленные капли дождя.

Опыт Юнга с конвертами. Вопрос о квантовом стирании данных

(управляет ли сознание материей)
В "опыте Юнга" электроны из электронной пушки пролетают через 1 или 2 щели в преграде и оставляют след на экране.
При пролете через одну щель электроны оставляют одну полоску на экране против щели, как будто, электрон - частица.
Интересное происходит при пролете через 2 щели в преграде.
Источник: https://levhudoi.blogspot.ru/2017/02/kvant.html
Электроны проявляют себя как волна (интерференционная картина из множества полос как результат наложения волн), если не наблюдать за тем, через какую щель пролетал каждый электрон.
А если наблюдать, через какую из 2 щелей пролетел каждый электрон, то на экране будет 2 полоски (то есть, электроны вели себя как частицы).
Получается 2 возможных варианта:
1. Поведение электрона зависит от того, наблюдал ли за ним человек или нет. То есть, сознание человека влияет на поведение электрона.
Либо
2. На электрон влияет то техническое устройство ("детектор"), которое фиксирует через какую щель он летит. (Далее информация передается человеку от детектора, и человек тут не при чем).
Чтобы разобраться с этим решили записывать данные с включенного детектора и картину на экране, но не сообщать всё это человеку.
Выяснилось. Если во время эксперимента не наблюдать за пролетом электронов через каждую щель, а записать показатели детекторов обоих щелей о пролете через них каждого электрона, но, эти данные не изучить человеком, а сразу уничтожить после эксперимента, то мы получим на экране волновую картину, а не две полоски. Это называется "стирание данных".
А, если, данные не уничтожать, а изучить после опыта, то, на экране получится 2 полоски напротив щелей.
Вот это стирание данных наиболее удивительно. Но, прежде чем разобраться с этим, надо точно выяснить - реальный ли это эксперимент или вымышленный?
Эксперимент имеет две стадии: сначала экспериментатор отмечает через какую прорезь прошел каждый фотон без нарушения движения, и демонстрирует нарушение интерференционной картины. Эта стадия показывает, что существует «путевая» информация, которая вызывает повреждение интерференционной картины, но нет механического нарушения (как полагалось в начале создания квантовой теории). Вторая стадия проходит, стирая «путевую» информацию, и демонстрируя, что интерференционная картина восстановлена.
В этой статье википедии нет ни одной ссылки. Я впервые такое вижу. Наверное, подлые электроны стерли ссылки, зная что за ними будут наблюдать читатели!
Я "обращаюсь к залу" с просьбой дать ссылки на наиболее авторитетные источники эффекта стирания данных или иначе "Эксперимент квантового ластика" . А я тоже продолжу поиски.
Из того что я накопал в интернете выходит, что в дискуссиях на русском языке народ разделился на 2 категории - одни считают, что хоть стирай данные, хоть не стирай, всё равно, на экране будут 2 полоски, другие считают что при стирании данных с детекторов на экране получится волновая картина с множеством полос (более 2).
Я брал инфу, в том числе, отсюда:
Опыт Юнга объясняет Том Кэмпбел.
Корпускулярно-волновой дуализм
Насколько авторитетен Том Кэмпбел - не знаю. Говорят он поклонник мистики. Как и другие люди в сети с неизвестной репутацией, которые утверждают то же, что и он.
В этом видео https://www.youtube.com/watch?v=SnQkTfSpfOU ("ДОКАЗАТЕЛЬСТВА ВИРТУАЛЬНОСТИ НАШЕГО МИРА") на времени 10:35 это называется эксперимент с "отложенным выбором" и что этот эксперимент проведен в 2006 году.

Зеркало Ллойда

Зе́ркало Лло́йда  — оптическая система для наблюдения интерференции световых волн . Эксперимент с зеркалом был впервые описан в 1834 году Ллойдом в Трудах Ирландской королевской академии наук . В эксперименте свет от источника монохроматического излучения отражается от поверхности зеркала под небольшим углом и интерферирует со светом, идущим непосредственно от источника. Таким образом, источниками когерентных волн служат реальный источник света и его мнимое изображение

Дифракционная решетка. Определение и основные сведения о дифракционной решетке

ОПРЕДЕЛЕНИЕ

Дифракционной решеткой называют спектральный прибор, который является системой некоторого количества щелей, разделенных непрозрачными промежутками.

Очень часто на практике используют одномерную дифракционную решетку, состоящую из параллельных щелей одинаковой ширины, находящихся в одной плоскости, которые разделяют равными по ширине непрозрачными промежутками. Такую решетку изготавливают при помощи специальной делительной машины, которая наносит на пластине из стекла параллельные штрихи. Количество таких штрихов может быть более чем тысяча на один миллиметр.

Лучшими считаются отражательные дифракционные решетки. Это совокупность участков, которые отражают свет с участками, которые свет отражают. Такие решетки представляют собой отшлифованную металлическую пластину, на которой рассеивающие свет штрихи нанесены резцом.

Картина дифракции на решетке — это результат взаимной интерференции волн, которые идут ото всех щелей. Следовательно, при помощи дифракционной решетки реализуется многолучевая интерференция когерентных пучков света, которые подверглись дифракции и которые идут от всех щелей.

Допустим, что на дифракционной решетке ширина щели будет a, ширина непрозрачного участка — b, тогда величина:

называется периодом (постоянной) дифракционной решетки.

Видео Опыт Юнга с Двумя щелями. Рус. Хорошее качество.

Опыт Юнга с двумя щелями. Опыт Юнга или эксперемент с двумя щелями

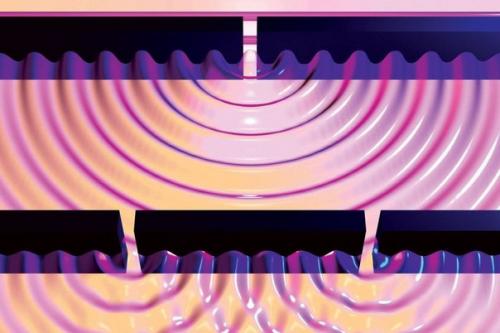
В опыте пучок света направляется на непрозрачный экран-ширму с двумя параллельными прорезями, позади которого устанавливается проекционный экран. Особенность прорезей в том, что их ширина приблизительно равна длине волны излучаемого света (влияние ширины прорезей на интерференцию рассматривается ниже). На проекционном экране получается целый ряд чередующихся интерференционных полос, что и было продемонстрировано Томасом Юнгом.

На проекционном экране получается целый ряд чередующихся интерференционных полос, что и было продемонстрировано Томасом Юнгом.
Если исходить из того, что свет состоит из частиц (корпускулярная теория света), то на проекционном экране можно было бы увидеть только две параллельные полосы света, прошедшие через прорези ширмы. Между ними проекционный экран оставался бы практически неосвещенным.
С другой стороны, если предположить, что свет представляет собой распространяющиеся волны (волновая теория света), то, согласно принципу Гюйгенса, каждая прорезь является источником вторичных волн.
Если вторичные волны достигнут линии в середине проекционного экрана, находящейся на равном удалении от прорезей, в одной фазе, то на серединной линии экрана их амплитуды сложатся, что создаст максимум яркости. То есть, максимум яркости окажется там, где, согласно корпускулярной теории, яркость должна быть практически нулевой.
С другой стороны, на определённом удалении от центральной линии волны окажутся в противофазе — их амплитуды компенсируются, что создаст минимум яркости (тёмная полоса). По мере дальнейшего удаления от средней линии яркость периодически изменяется, возрастая до максимума и снова убывая.

Интерференционная картина возникает на экране, когда ширина прорезей близка к длине волны излучаемого монохроматического света. Если ширину прорезей увеличивать, то освещённость экрана будет возрастать, но контраст интерференционной картины будет падать вплоть до полного её исчезновения.

Интерференция света.

Необходимы более веские доказательства того, что свет при распространении ведет себя как волна. Любому волновому движению присущи явления интерференции и дифракции. Для того чтобы быть уверенным в том, что свет имеет волновую природу, необходимо найти экспериментальные доказательства интерференции и дифракции света.

Интерференция — достаточно сложное явление . Чтобы лучше понять его суть, мы вначале остановимся на интерференции механических волн.

Сложение волн. Очень часто в среде одновременно распространяется несколько различных волн. Например, когда в комнате беседуют несколько человек, то звуковые волны накладываются друг на друга. Что при этом происходит?

Проще всего проследить за наложением механических волн, наблюдая волны на поверхности воды. Если мы бросим в воду два камня, создав этим две кольцевые волны, то нетрудно заметить, что каждая волна проходит сквозь другую и ведет себя в дальнейшем так, как будто бы другой волны совсем не существовало. Точно так же любое число звуковых волн может одновременно распространяться в воздухе, ничуть не мешая друг другу. Множество музыкальных инструментов в оркестре или голосов в хоре создают звуковые волны, одновременно улавливаемые нашим ухом. Причем ухо в состоянии отличить один звук от другого.

Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются друг на друга. Наблюдая волны на поверхности воды от двух брошенных в воду камней, можно заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если две волны встречаются в одном месте гребнями, то в этом месте возмущение поверхности воды усиливается.

Если же, напротив, гребень одной волны встречается с впадиной другой, то поверхность воды не будет возмущена.

Вообще же в каждой точке среды колебания, вызванные двумя волнами, просто складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую (т. е. с учетом их знаков) сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.

Интерференция. Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний, называется интерференцией.
Выясним, при каких условиях имеет место интерференция волн. Для этого рассмотрим более подробно сложение волн, образуемых на поверхности воды.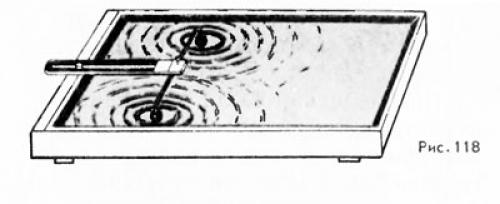

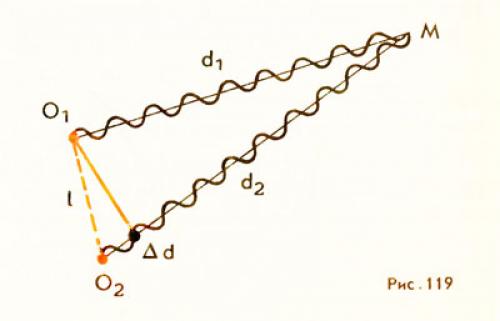
Можно одновременно возбудить две круговые волны в ванне с помощью двух шариков, укрепленных на стержне, который совершает гармонические колебания (рис. 118). В любой точке М на поверхности воды (рис. 119) будут складываться колебания, вызванные двумя волнами (от источников O1и О2). Амплитуды колебаний, вызванных в точке М обеими волнами, будут, вообще говоря, отличаться, так как волны проходят различные пути d1и d2. Но если расстояние l между источниками много меньше этих путей  (l « d1  и l « d2) ,   то обе амплитуды
можно считать практически одинаковыми.

Результат сложения волн, приходящих в точку M, зависит от разности фаз между ними. Пройдя различные расстояния d1и d2, волны имеют разность хода Δd = d2—d1. Если разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой ровно на один период (как раз за период волна проходит путь, равный длине волны). Следовательно, в этом случае гребни (как и впадины) обеих волн совпадают.

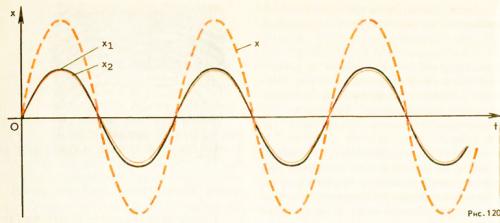
Условие максимумов. На рисунке 120 изображена зависимость от времени смещений X1и X2, вызванных двумя волнами при Δd= λ. Разность фаз колебаний равна нулю (или, что то же самое, 2л, так как период синуса равен 2п). В результате сложения этих колебаний возникает результирующее колебание с удвоенной амплитудой. Колебания результирующего смещения на рисунке показаны цветом (пунктир). То же самое будет происходить, если на отрезке Δd укладывается не одна, а любое целое число длин волн.

Амплитуда колебаний среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн:

 Δd=κλ

где к=0,1,2,….

Условие минимумов. Пусть теперь на отрезке Δd укладывается половина длины волны. Очевидно, что при этом вторая волна отстает от первой на половину периода. Разность фаз оказывается равной п, т. е. колебания будут происходить в противофазе. В результате сложения этих колебаний амплитуда результирующего колебания равна нулю, т. е. в рассматриваемой точке колебаний нет (рис. 121). То же самое произойдет, если на отрезке укладывается любое нечетное число полуволн.
Амплитуда колебаний среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:

Δd=(2к+1)λ/2

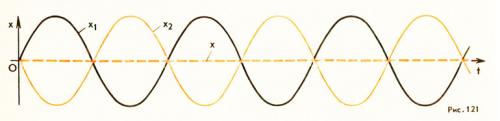
Если разность хода d2— d1принимает промежуточное значение
между λ и λ/2 , то и амплитуда результирующего колебания принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но наиболее важно то, что Амплитуда колебаний в любой точке he меняется с течением времени. На поверхности воды возникает определенное, неизменное во времени распределение амплитуд колебаний, которое называют интерференционной картиной. На рисунке 122 показан рисунок с фотографии интерференционной картины двух круговых волн от двух источников (черные кружки). Белые участки в средней части фотографии соответствуют максимумам колебаний, а темные — минимумам.
Когерентные волны. Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебаний была постоянной.
Источники, удовлетворяющие этим условиям, называются когерентными. Когерентными называют и созданные ими волны. Только при сложении когерентных волн образуется устойчивая интерференционная картина.
Если же разность фаз колебаний источников не остается постоянной, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет меняться. Поэтому амплитуда результирующих колебаний с течением времени изменяется. В результате максимумы и минимумы перемещаются в пространстве и интерференционная картина размывается.

Зеркала Френеля

S  — точечный источник света;
Z1, Z2  — зеркала;
S1, S2  — мнимые изображения источника света;
E  — экран;
D  — область перекрытия потоков света от мнимых источников, где наблюдается интерференция;
B  — бленда для защиты от засветки экрана источником света.
Для наглядности угол между зеркалами на рисунке утрированно увеличен.

Устройство состоит из двух плоских зеркал Z1 и Z2 , образующих двугранный угол, отличающийся от 180° всего на несколько угловых минут . При освещении зеркал от источника S отражённые от зеркал пучки лучей можно рассматривать как исходящие из когерентных источников S1 и S2 , являющихся мнимыми изображениями S . В пространстве, где пучки перекрываются, возникает интерференция. Если источник S линеен (щель) и параллелен вершине двугранного угла, образованного зеркалами, то при освещении зеркал монохроматическим светом на экране E , который может быть установлен в любом месте в области перекрытия пучков, наблюдается интерференционная картина в виде равноотстоящих тёмных и светлых полос, параллельных щели. По расстоянию между полосами и величине двугранного угла можно определить длину волны света.

Опыты, проведённые с этим прибором явились одним из решающих доказательств волновой природы света.